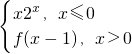Question

设函数f（x）满足f（-x）=f（x），且当x≥0时，f(x)=(

1

4

)x，又函数g（x）=|xsinπx|，则函数h（x）=f（x）-g（x）在[-

1

2

，2]上的零点个数为（　　）

A．3

B．4

C．5

D．6

Answer 1

分析：依题意可知，f（x）、g（x）均为偶函数，将h（x）=f（x）-g（x）在[-

1

2

，2]上的零点个数转化为f（x）、g（x）在[-

1

2

，2]上的交点个数即可．

解答：解：∵f（-x）=f（x），
∴f（x）为偶函数；
又g（x）=|xsinπx|，
同理可得g（x）为偶函数．
令h（x）=f（x）-g（x）=0，x∈[-

1

2

，2]，
则h（x）=f（x）-g（x）在[-

1

2

，2]上的零点个数就是函数f（x）与g（x）在[-

1

2

，2]上的交点个数．
当x=0时，f（0）=(

1

4

)0=1，g（0）=|0×sin0|=0，f（0）＞g（0）；
当x=

1

2

时，f（

1

2

）=(

1

4

)

1

2

=

1

2

，g（

1

2

）=|

1

2

×sin

π

2

|=

1

2

，f（

1

2

）=g（

1

2

），
∴f（x）与g（x）在[0，

1

2

]上有一个交点；
同理可得，f（x）与g（x）在[

1

2

，1]，[1，

3

2

]，[

3

2

，2]上各有一个交点；
又f（x）、g（x）均为偶函数，
∴f（x）与g（x）在[-

1

2

，0]上有一个交点；
综上所述，f（x）与g（x）在[-

1

2

，2]上有五个交点．
故选C．

点评：本题考查根的存在性及根的个数判断，考查函数的奇偶性，考查转化思想与抽象思维能力的综合应用，属于难题．