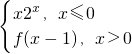题目内容
设函数f(x)满足f(﹣x)=f(x),且当x≥0时,![]() ,又函数g(x)=|xsinπx|,则函数h(x)=f(x)﹣g(x)在
,又函数g(x)=|xsinπx|,则函数h(x)=f(x)﹣g(x)在![]() 上的零点个数为( )
上的零点个数为( )
|
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
|
C 【解析】∵f(﹣x)=f(x), ∴f(x)为偶函数; 又g(x)=|xsinπx|, 同理可得g(x)为偶函数. 令h(x)=f(x)﹣g(x)=0,x∈[﹣ 则h(x)=f(x)﹣g(x)在[﹣ 当x=0时,f(0)= 当x= ∴f(x)与g(x)在[0, 同理可得,f(x)与g(x)在[ 又f(x)、g(x)均为偶函数, ∴f(x)与g(x)在[﹣ 综上所述,f(x)与g(x)在[﹣ 故选C. |