题目内容
设函数f(x)定义在实数集上，它的图象关于直线x＝1对称，且当x≥1时，f(x)＝3x－1，则有( )
(A)f(
)＜f(
)＜f(
)
(B)f()＜f()＜f(
)
(C)f()＜f()＜f()
(D)f()＜f()＜f()
B.由已知条件可得f(x)＝f(2－x).
∴f()＝f(
)，f()＝f(
).
又x≥1时，f(x)＝3x－1，
在(1，＋∞)上递增，∴f()＞f()＞f().
即f()＞f()＞f().
【方法技巧】具有对称性、奇偶性、周期性函数的函数值大小比较的常用方法：
(1)单调性法：先利用相关性质，将待比较函数值调节到同一单调区间内，然后利用该函数在该区间上的单调性比较大小.
(2)图象法：先利用相关性质作出函数的图象，再结合图象比较大小.
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
，
．
的大小关系；
对任意x＞0成立？若存在，求出x0的取值范围；若不存在，请说明理由．
，求a的取值范围. 
)<f(2)<f(
) B．f(
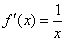，g(x)=f(x)+f′(x)，
的大小关系；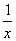
对任意x＞0成立？若存在，求出x0的取值范围；若不存在，请说明理由。