题目内容
已知函数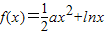 ,其中a∈R.
,其中a∈R.(Ⅰ)求f(x)的单调区间;
(Ⅱ)若f(x)在(0,1]上的最大值是-1,求a的值.
【答案】分析:(1)先求导数,分a≥0和a<0进行讨论根据导数的正负可得单调区间;
(2)分类讨论求得f(x)在(0,1]上的最大值,令其为1,可得a的值.
解答:解:(1)由题意可得函数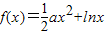 的定义域为(0,+∞)
的定义域为(0,+∞)
由求导公式可得: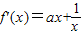 =
=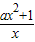
当,f′(x)= >0,f(x)在(0,+∞)单调递增;
>0,f(x)在(0,+∞)单调递增;
当a<0时,令 >0,可解得x<
>0,可解得x<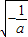 ,即f(x)在(0,
,即f(x)在(0,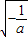 )单调递增,
)单调递增,
同理由 <0,可解得x>
<0,可解得x>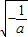 ,即f(x)在(
,即f(x)在(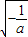 ,+∞)单调递减.
,+∞)单调递减.
(2)由(1)可知:若a≥0时,f(x)在(0,1]单调递增,
故函数在x=1处取到最大值f(1)=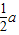 =-1,解得a=-2,与a≥0矛盾应舍去;
=-1,解得a=-2,与a≥0矛盾应舍去;
若0<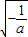 ≤1,即a≤-1,函数f(x)在(0,
≤1,即a≤-1,函数f(x)在(0,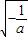 )单调递增,在(
)单调递增,在(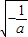 ,+∞)单调递减.
,+∞)单调递减.
故若 >1,即-1<a<0时,f(x)在(0,1]单调递增,
>1,即-1<a<0时,f(x)在(0,1]单调递增,
故函数在x=1处取到最大值f(1)= =-1,解得a=-2,应舍去.
=-1,解得a=-2,应舍去.
综上可得所求a的值为:-e
点评:本题为函数与导数的综合应用,正确的分类讨论是解决问题的关键,属中档题.
(2)分类讨论求得f(x)在(0,1]上的最大值,令其为1,可得a的值.
解答:解:(1)由题意可得函数
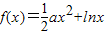 的定义域为(0,+∞)
的定义域为(0,+∞)由求导公式可得:
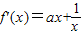 =
=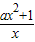
当,f′(x)=
 >0,f(x)在(0,+∞)单调递增;
>0,f(x)在(0,+∞)单调递增;当a<0时,令
 >0,可解得x<
>0,可解得x<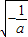 ,即f(x)在(0,
,即f(x)在(0,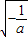 )单调递增,
)单调递增,同理由
 <0,可解得x>
<0,可解得x>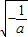 ,即f(x)在(
,即f(x)在(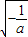 ,+∞)单调递减.
,+∞)单调递减.(2)由(1)可知:若a≥0时,f(x)在(0,1]单调递增,
故函数在x=1处取到最大值f(1)=
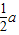 =-1,解得a=-2,与a≥0矛盾应舍去;
=-1,解得a=-2,与a≥0矛盾应舍去;若0<
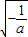 ≤1,即a≤-1,函数f(x)在(0,
≤1,即a≤-1,函数f(x)在(0,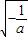 )单调递增,在(
)单调递增,在(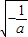 ,+∞)单调递减.
,+∞)单调递减.故若
 >1,即-1<a<0时,f(x)在(0,1]单调递增,
>1,即-1<a<0时,f(x)在(0,1]单调递增,故函数在x=1处取到最大值f(1)=
 =-1,解得a=-2,应舍去.
=-1,解得a=-2,应舍去.综上可得所求a的值为:-e
点评:本题为函数与导数的综合应用,正确的分类讨论是解决问题的关键,属中档题.

练习册系列答案
相关题目
 ,其中a∈R.
,其中a∈R. ,其中a∈R.
,其中a∈R. ,其中a∈R.
,其中a∈R.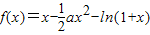 ,其中a∈R.
,其中a∈R. ,其中a∈R.
,其中a∈R.