题目内容
3.函数y=cos(2x-$\frac{π}{3}$)的最小正周期是( )| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
分析 由条件利用函数y=Acos(ωx+φ)的周期为$\frac{2π}{ω}$,求得结果.
解答 解:∵y=cos(2x-$\frac{π}{3}$),
∴函数y=cos(2x-$\frac{π}{3}$)的最小正周期T=$\frac{2π}{2}$=π.
故选:B.
点评 本题主要考查函数y=Acos(ωx+φ)的周期性,利用了函数y=Acos(ωx+φ)的周期为$\frac{2π}{ω}$,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.若a=log20.5,b=20.5,c=0.52,则a,b,c三个数的大小关系是( )
| A. | a<b<c | B. | b<c<a | C. | a<c<b | D. | c<a<b |
8.已知正方体ABCD-A1B1C1D1内有一个内切球O,则在正方体ABCD-A1B1C1D1内任取点M,点M在球O内的概率是( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{8}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
15.已知向量$\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(1,-2),则$\overrightarrow{a}$•$\overrightarrow{b}$的值为( )
| A. | -4 | B. | 8 | C. | -1 | D. | -7 |
13.函数f(x)=log2x+x-2的零点所在区间为[m,m+1](m∈Z),则m的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
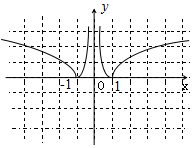 已知函数f(x)是定义在{x|x≠0}上的偶函数,且当x>0时,f(x)=log2x.
已知函数f(x)是定义在{x|x≠0}上的偶函数,且当x>0时,f(x)=log2x.