题目内容
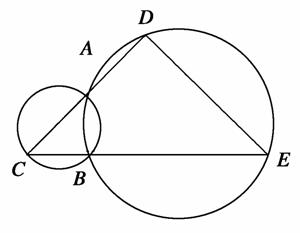
如图,AB是两圆的交点,AC是小圆的直径,D和E分别是CA和CB的延长线与大圆的交点,已知AC=4,BE=10,且BC=AD,则DE=( )
A.6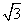 B.6
B.6
C.8 D.6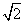
A
[解析] 设CB=AD=x,则由割线定理,
得CA·CD=CB·CE,即4(4+x)=x(x+10),
化简得x2+6x-16=0,解得x=2或x=-8(舍去),
即CD=6,CE=12,
因为CA为直径,所以∠CBA=90°,即∠ABE=90°,
则由圆的内接四边形对角互补,得∠D=90°,
则CD2+DE2=CE2(勾股定理)∴62+DE2=122,
∴DE=6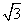 .
.

练习册系列答案
相关题目


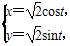 (t为参数),C在点(1,1)处的切线为l,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,则l的极坐标方程为________.
(t为参数),C在点(1,1)处的切线为l,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,则l的极坐标方程为________.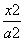 -
-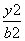 =1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )
=1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )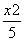 -
-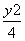 =1 B.
=1 B.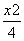 -
-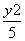 =1
=1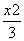 -
-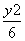 =1 D.
=1 D.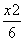 -
-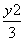 =1
=1