题目内容
已知动点P到点F(1,0)的距离比到直线l:x+2=0距离小1.设动点P的轨迹为C,
(Ⅰ)求轨迹C的方程;
(Ⅱ)已知定点M(4,0).斜率为k的直线交轨迹C于A、B两点,使△ABM成为以AB为底边的等腰三角形,
①求斜率k的取值范围;
②求弦长|AB|的最大值.
解:(Ⅰ)设P(x,y),由题意可得,P在直线x+2=0右边,
所以P点到直线x= -1和到F(1,0)距离相等,
所以P点的轨迹是顶点在原点, F为焦点,开口向右的抛物线,
∵F和顶点的距离=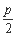 =1,2p=4,所以轨迹C的方程是y²=4x 4分
=1,2p=4,所以轨迹C的方程是y²=4x 4分
(Ⅱ) ①设直线AB的方程为y=kx+b,联立抛物线y2=4x,消元得:k2x2+(2kb-4)x+b2=0,
设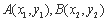 及AB中点为
及AB中点为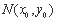 ,
,
则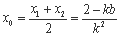 ,y0=kx0+b=
,y0=kx0+b=
∵AM=BM,∴MN⊥AB,∴kMN·kAB= -1,即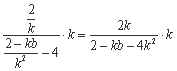 = -1,
= -1,
得2-kb=2k2,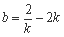 ,
,
由△=-kb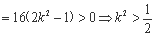 ,
,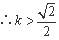 或
或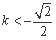 ,
,
②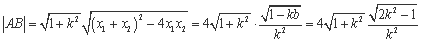
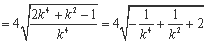
令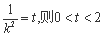 ,
,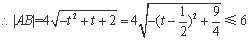
所以弦长的最大值为

练习册系列答案
相关题目
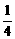 的等差数列,
的等差数列,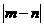 等于
等于 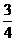 C.
C. D.
D.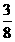
 单调递增区间是 .
单调递增区间是 .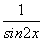 ≥4
≥4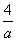 ≥-4
≥-4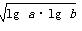
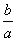 +
+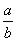 ≥2
≥2 则
则 的最大值是________.
的最大值是________.