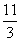题目内容
已知f(x)为定义在R上的偶函数,当x≥0时,有f(x+1)=-f(x),且当x∈[0,1)时,f(x)=log2(x+1),给出下列命题:
①f(2 013)+f(-2 014)的值为0;
②函数f(x)在定义域上为周期是2的周期函数;
③直线y=x与函数f(x)的图象有1个交点;
④函数f(x)的值域为(-1,1).
其中正确命题的序号有________.
①③④
[解析] 当x∈[1,2)时,x-1∈[0,1),f(x)=-f(x-1)=-log2x,且x≥0时,f(x)=f(x+2),f(x)又是R上的偶函数.作出函数f(x)的部分图象如图,由图可知,②错误,③④都正确,f(2 013)=f(1)=-f(0)=0,f(2 014)=f(0)=0,所以f(2 013)+f(-2 014)=0,①正确,故正确的命题序号是①③④.


练习册系列答案
相关题目
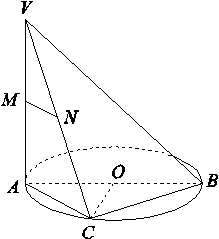
 的图象大致是( )
的图象大致是( )

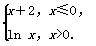 若函数y=|f(x)|-k(x+e2)的零点恰有四个,则实数k的值为( )
若函数y=|f(x)|-k(x+e2)的零点恰有四个,则实数k的值为( )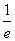

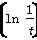 ≤2f(1),那么t的取值范围是________.
≤2f(1),那么t的取值范围是________.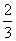 ,P(ξ=x2)=
,P(ξ=x2)=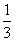 ,且x1<x2,又已知E(ξ)=
,且x1<x2,又已知E(ξ)=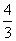 ,D(ξ)=
,D(ξ)= ,则x1+x2的值为( )
,则x1+x2的值为( )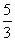 B.
B.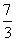 C.3 D.
C.3 D.