题目内容
8.若不等式$\left\{\begin{array}{l}{x-1>{a}^{2}}\\{x-4<2a}\end{array}\right.$的解集不是空集,则实数a的取值范围是( )| A. | (-1,3) | B. | (-∞,-1)∪(3,+∞) | C. | (-3,1) | D. | (-∞,-3)∪(1,+∞) |
分析 由题意可得a2+1<2a+4,由此求得a的范围.
解答 解:不等式$\left\{\begin{array}{l}{x-1>{a}^{2}}\\{x-4<2a}\end{array}\right.$,即$\left\{\begin{array}{l}{x{>a}^{2}+1}\\{x<2a+4}\end{array}\right.$,根据它的解集非空,可得a2+1<2a+4,
求得-1<a<3,
故选:A.
点评 本题主要考查其它不等式的解法,交集非空的条件,属于基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
18.函数y=$\sqrt{9-{3^x}}$的值域是( )
| A. | [0,+∞) | B. | [0,3] | C. | [0,3) | D. | (0,3) |
 将钟表上的时针作为角的始边,分针作为终边,那么当钟表上显示8点零5分时,求时针与分针构成的角度.
将钟表上的时针作为角的始边,分针作为终边,那么当钟表上显示8点零5分时,求时针与分针构成的角度.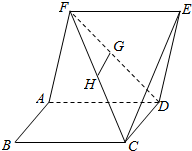 如图.已知正方形ABCD与ADEF边长都为1,且平面ADEF⊥平面ABCD,G,H是DF,FC的中点.
如图.已知正方形ABCD与ADEF边长都为1,且平面ADEF⊥平面ABCD,G,H是DF,FC的中点.