题目内容
已知：a∈R+,求证：a+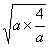
≥
.
证明：∵a∈R+，设t=a+4a≥2=4,则左式=f(t)=t+(t≥4)
∴f(t)=(
)2+2在t≥4上递增.
∴f(t)≥f(4)=4+
=
得证.
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
≥.桃李文化快乐暑假武汉出版社系列答案优秀生快乐假期每一天全新寒假作业本系列答案题目内容
已知：a∈R+,求证：a+≥.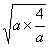
证明：∵a∈R+，设t=a+4a≥2=4,则左式=f(t)=t+(t≥4)
∴f(t)=()2+2在t≥4上递增.
∴f(t)≥f(4)=4+=得证.
桃李文化快乐暑假武汉出版社系列答案优秀生快乐假期每一天全新寒假作业本系列答案
D，同时满足：
不存在“和谐区间”．
(a∈R，a≠0)有“和谐区间”[m，n]，当a变化时，求出n－m的最大值．
(a∈R)．
．