题目内容

设数列{an}的首项a1=a≠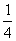,且an+1=记bn=a2n-1-,n=1,2,3,….

(1)求a2,a3;

(2)判断数列{bn}是否为等比数列,并证明你的结论;

(3)求(b1+b2+…+bn).

解：(1)a2=a1+=a+,?

a3=a2=a+.?

(2)因为a4=a3+=a+,

所以a5=a4=a+.

所以b1=a1-=a-≠0,b2=a3-=(a-),b3=a5-=(a-).

猜想:{bn}是公比为的等比数列.

证明如下:?

因为bn+1=a2n+1-

=a2n-

=(a2n-1+)-

=(a2n-1-)

=bn(n∈N*),?

所以{bn}是首项为a-,公比为的等比数列.?

(3)(b1+b2+…+bn)=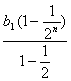==2(a-).

练习册系列答案
相关题目
设数列{an}的首项a1=
3
2
，前n项和为Sn，且满足2an+1+Sn=3（ n∈N*）．
（Ⅰ）求a2及an；
（Ⅱ）求满足
18
17
＜
S2n
Sn
＜
8
7
的所有n的值．
设数列{an}的首项a1=a≠
1
4
，且an+1=
1
2
an		(n为偶数)
an+
1
4
(n为奇数)
，n∈N*，记bn=a2n-1-
1
4
，cn=
sinn
|sinn|
bn，n∈N*．
（1）求a2，a3；
（2）判断数列{bn}是否为等比数列，并证明你的结论；
（3）当a＞
1
4
时，数列{cn}前n项和为Sn，求Sn最值．
设数列{an}的首项a1=
1
2
，且an+1=
2an
1+an
（n∈N*）．
（1）求a2，a3，a4；
（2）根据上述结果猜想数列{an}的通项公式，并用数学归纳法加以证明．
（2012•昌平区二模）设数列{an}的首项a1=-
1
2
，前n项和为Sn，且对任意n，m∈N*都有
Sn
Sm
=
n(3n-5)
m(3m-5)
，数列{an}中的部分项{abk}(k∈N*）成等比数列，且b1=2，b2=4．
（Ⅰ）求数列{an}与{bn}与的通项公式；
（Ⅱ）令f(n)=
1
bn+1
，并用x代替n得函数f（x），设f（x）的定义域为R，记cn=f(0)+f(
1
n
)+f(
2
n
)+…+f(
n
n
)(n∈N*)，求
n
i=1
1
cici+1
．
设数列{an}的首项a1=
5
4
，且an+1=
1
2
an，n为偶数
an+
1
4
，n为奇数
，记bn=a2n-1-
1
4
，n=1，2，3，…
（Ⅰ）求数列{bn}的通项公式；
（Ⅱ）若设数列{cn}的前n项和为Sn，cn=nbn，求Sn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网