题目内容
13.P(x,y)是圆x2+y2=1与直线x+y+2m=0(m>0)的公共点,则直线mx-y-2008=0的倾斜角的最大值为45°.分析 根据圆x2+y2=1与直线x+y+2m=0(m>0)有公共点求出m的范围,进而根据直线斜率与倾斜角的关系,得到答案.
解答 解:圆x2+y2=1与直线x+y+2m=0(m>0)有公共点,
则圆心(0,0)到直线x+y+2m=0的距离d=$\frac{2m}{\sqrt{2}}$=$\sqrt{2}m$≤1,
解得:m∈(0,$\frac{\sqrt{2}}{2}$],
又由直线mx-y-2008=0的斜率为m,
故当m=$\frac{\sqrt{2}}{2}$时,直线mx-y-2008=0的倾斜角的最大值为45°,
故答案为:45°.
点评 本题考查的知识点是直线与圆的位置关系,直线的斜率与倾斜角,难度中档.

练习册系列答案
相关题目
4.已知x,y满足不等式$\left\{\begin{array}{l}{x≥0}\\{x-y+2≤0}\\{2x+y-5≤0}\end{array}\right.$,则z=(x-1)2+y2的最小值为( )
| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{9}{2}$ | C. | $\sqrt{5}$ | D. | 5 |
1.数列{an}的前n项和Sn=n2+2n(n∈N*),若m-n=5,则am-an=( )
| A. | 2 | B. | 5 | C. | -5 | D. | 10 |
8.已知数列{an}是以a为首项,a为公比的等比数列(a>0,a≠1),令bn=an1gan,若{bn}中的每一项总小于它后面的一项,则a的取值范围是( )
| A. | (0,$\frac{1}{2}$) | B. | (1,+∞) | C. | (0,$\frac{1}{2}$)∪(1,+∞) | D. | (0,1)∪(1,+∞) |
14.化简$\frac{sinθ}{{\sqrt{1-{{sin}^2}θ}}}+\frac{{\sqrt{1-{{cos}^2}θ}}}{cosθ}(\frac{π}{2}<θ<π)$的结果是( )
| A. | 0 | B. | 2tanθ | C. | -2tanθ | D. | $\frac{1}{2tanθ}$ |
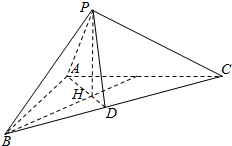 如图,三棱锥P-ABC中,AB=6,AC=8,D是BC的中点,AD=$\frac{1}{2}$BC,P在平面ABC上的射影H是△ABC的重心,PH=4.
如图,三棱锥P-ABC中,AB=6,AC=8,D是BC的中点,AD=$\frac{1}{2}$BC,P在平面ABC上的射影H是△ABC的重心,PH=4.