题目内容
在R上定义运算*:x*y=x(y+1).若不等式(kx)*x<1对于任意实数x恒成立,则实数k的取值范围是( )
分析:由题意可得 kx(x+1)<1恒成立,即 kx2+kx-1<0恒成立,故有k=0,或
.由此求得实数k的取值范围.
|
解答:解:由不等式(kx)*x<1对于任意实数x恒成立,可得 kx(x+1)<1恒成立,
即 kx2+kx-1<0恒成立,故有k=0,或
.
解得 4<k≤0,
故选B.
即 kx2+kx-1<0恒成立,故有k=0,或
|
解得 4<k≤0,
故选B.
点评:本题主要考查新定义、函数的恒成立问题、二次函数的性质应用,属于中档题.

练习册系列答案
相关题目
 :x
:x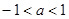 B.0<
B.0< <2 C.
<2 C. D.
D.
 :x
:x B.
B. C.
C. D.
D.