题目内容
5.变量x,y满足$\left\{{\begin{array}{l}{3x-y-2≥0}\\{x+2y-3≥0}\\{4x+y-12≤0}\end{array}}\right.$,则(x-3)2+(y-3)2的范围是[$\frac{9}{17},9$].分析 由约束条件画出可行域,然后利用(x-3)2+(y-3)2的几何意义,即可行域内的动点与定点(3,3)距离的平方求解.
解答 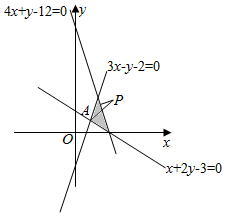 解:由约束条件$\left\{{\begin{array}{l}{3x-y-2≥0}\\{x+2y-3≥0}\\{4x+y-12≤0}\end{array}}\right.$作出可行域如图,
解:由约束条件$\left\{{\begin{array}{l}{3x-y-2≥0}\\{x+2y-3≥0}\\{4x+y-12≤0}\end{array}}\right.$作出可行域如图,
联立$\left\{\begin{array}{l}{3x-y-2=0}\\{x+2y-3=0}\end{array}\right.$,解得A(1,1).
(x-3)2+(y-3)2的几何意义为可行域内的动点与定点(3,3)距离的平方.
∵|PA|=$\sqrt{(3-1)^{2}+(3-1)^{2}}=\sqrt{8}$,
而P到x轴上的点(3,0)的距离为3,
点P(3,3)到直线4x+y-12=0的距离为$\frac{|4×3+3-12|}{\sqrt{17}}=\frac{3}{\sqrt{17}}$.
∴(x-3)2+(y-3)2的范围是[$\frac{9}{17},9$].
故答案为:[$\frac{9}{17},9$].
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法和数学转化思想方法,是中档题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
15.设全集U=R,集合A={x|y=lgx},B={-1,1},则下列结论正确的是( )
| A. | A∩B={-1} | B. | (∁RA)∪B=(-∞,0) | C. | A∪B=(0,+∞) | D. | (∁RA)∩B={-1} |
17.方程x2+y2+2ax-4y+(a2+a)=0表示一个圆,则a的取值范围是( )
| A. | [4,+∞) | B. | (4,+∞) | C. | (-∞,4] | D. | (-∞,4) |
14.把函数y=sin3x的图象向右平移$\frac{π}{4}$个长度单位,所得曲线的对应函数式( )
| A. | y=sin(3x-$\frac{3π}{4}$) | B. | y=sin(3x+$\frac{π}{4}$) | C. | y=sin(3x-$\frac{π}{4}$) | D. | y=sin(3x+$\frac{3π}{4}$) |