题目内容
若直线 截得的弦最短,则直线
截得的弦最短,则直线 的方程是
的方程是
A. | B. |
C. | D. |
D
解析试题分析:直线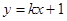 过定点
过定点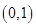 ,圆
,圆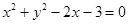 的圆心
的圆心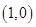 ,半径
,半径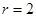 ,定点
,定点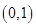 在圆的内部,所以连接定点和圆心的直线斜率为
在圆的内部,所以连接定点和圆心的直线斜率为 ,当直线
,当直线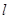 与该直线垂直时,弦长最短,此时
与该直线垂直时,弦长最短,此时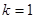 ,所以直线为
,所以直线为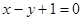
考点:直线与圆相交的弦长问题
点评:本题要满足弦长最短只需要圆心到直线的距离最大,关键点在于直线过定点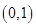 。所以圆心到直线的最大距离即为圆心到定点
。所以圆心到直线的最大距离即为圆心到定点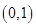 的距离
的距离

练习册系列答案
相关题目
若直线 平分圆
平分圆 ,则
,则 的最小值是
的最小值是
A. | B. | C. | D. |
若实数 满足
满足 ,
, 的取值范围为( ).
的取值范围为( ).
A. | B. | C. | D. |
圆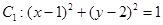 ,圆
,圆 ,则这两圆公切线的条数
,则这两圆公切线的条数
为 ( )
| A.1 | B.2 | C.3 | D.4 |
直线 截圆
截圆 所得劣弧所对的圆心角是
所得劣弧所对的圆心角是
A.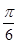 | B. |
C. | D. |
圆C1:(x-2)2+(y+2)2=9与圆C2:(x+1)2+(y-2)2=4的公切线有( )
| A.0条 | B.2条 | C.3条 | D.4条 |
若直线 与圆
与圆 相交于
相交于 两点,且
两点,且 (其中
(其中 为原点),则
为原点),则 的值为( )
的值为( )
A. 或 或 | B. | C. 或 或 | D. |
在平面直角坐标系 中,直线
中,直线 与圆
与圆 相交于
相交于 两点,则弦
两点,则弦 的长等于( )
的长等于( )
A. | B. | C.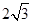 | D.1 |
圆 和
和 的位置关系为( )
的位置关系为( )
| A.外切 | B.内切 | C.外离 | D.内含 |