题目内容
圆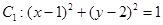 ,圆
,圆 ,则这两圆公切线的条数
,则这两圆公切线的条数
为 ( )
| A.1 | B.2 | C.3 | D.4 |
B
解析试题分析:根据题意,由于圆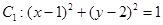 ,圆心(1,2),半径为1,而圆
,圆心(1,2),半径为1,而圆 的圆心为(2,5),半径为3,可知圆心距为d
的圆心为(2,5),半径为3,可知圆心距为d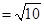 ,3-1<d<3+1,故可知两圆相交,则可知两圆公切线的条数为2,故选B.
,3-1<d<3+1,故可知两圆相交,则可知两圆公切线的条数为2,故选B.
考点:两圆公切线
点评:判定两圆的共切线的条数,主要是看两圆的位置关系,然后来得到证明,最多4条,相离时,最少外切是一条。属于基础题。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知 ,则以
,则以 为直径的圆的方程是( )
为直径的圆的方程是( )
A. | B. |
C. | D. |
已知圆O: ,直线
,直线 过点
过点 ,且与直线OP垂直,则直线
,且与直线OP垂直,则直线 的方程为( )
的方程为( )
A. | B. | C. | D. |
若过定点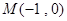 且斜率为
且斜率为 的直线与圆
的直线与圆 在第一象限内的部分有交点,则
在第一象限内的部分有交点,则 的取值范围是( ).
的取值范围是( ).
A. | B.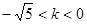 |
C. | D. |
已知圆 :
: ,过
,过 轴上的点
轴上的点 存在圆
存在圆 的割线
的割线 ,使得
,使得 ,则点
,则点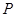 的横坐标
的横坐标 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
若直线 截得的弦最短,则直线
截得的弦最短,则直线 的方程是
的方程是
A. | B. |
C. | D. |
一束光线从点 出发经
出发经 轴反射,到达圆C:
轴反射,到达圆C: 上一点的最短路程是( )
上一点的最短路程是( )
| A.4 | B.5 |
C.3 -1 -1 | D.2 |
 中,圆
中,圆 的方程为
的方程为 ,若直线
,若直线 上至少存在一点,使得以该点为圆心,1为半径的圆与圆
上至少存在一点,使得以该点为圆心,1为半径的圆与圆 的取值范围是( )
的取值范围是( )
 或
或
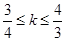
 或
或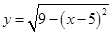 的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为该等比数列的公比的数是( )
的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为该等比数列的公比的数是( )


