题目内容
若函数y=bsin2x+a（b＜0）的最大值是4，最小值是-2，求a，b的值．
考点：三角函数的最值
专题：计算题,三角函数的图像与性质
分析：根据条件构建a、b的方程组解决，要注意条件中的b＜0，当sin2x取最大值时，函数y=bsin2x+a取得最小值，当sin2x取最小值时，函数y=bsin2x+a取得最大值．
解答：
解：∵b＜0，∴函数y=bsin2x+a的最大值为-b+a，最小值为b+a，
∵函数y=bsin2x+a（b＜0）的最大值是4，最小值是-2，
∴-b+a=4，b+a=-2，
解得：a=1，b=-3．
∵函数y=bsin2x+a（b＜0）的最大值是4，最小值是-2，
∴-b+a=4，b+a=-2，
解得：a=1，b=-3．
点评：本题考查了正弦型函数最值的求法，考查了方程思想．
练习册系列答案
相关题目
在△ABC中，AB=AC=2，BC=2
，则
•
=（ ）
| 3 |
| AB |
| AC |
A、2
| ||
| B、2 | ||
C、-2
| ||
| D、-2 |
在等比数列{an}中，若a2•a4•a12=64，则a6等于（ ）
| A、1 | B、2 | C、3 | D、4 |
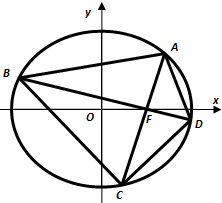已知椭圆Γ：
四棱锥S-ABCD，底面ABCD为平行四边形，侧面SBC⊥底面ABCD．已知∠DAB=135°，BC=2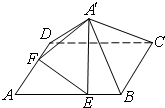
如图，已知正方形ABCD的边长为6，点E，F分别在边AB，AD上，AE=AF=4，现将△AEF沿线段EF折起到△A′EF位置，使得A′C=2