题目内容
将半径为R的圆面剪切去如图中的阴影部分,沿图所画的线折成一个正三棱锥,这个正三棱锥的侧面与底面所成的二面角的余弦值是( )
A. | B. |
C. | D. |
A
解析试题分析:因为根据题意可知,半径为R的圆面剪切去如图中的阴影部分,沿图所画的线折成一个正三棱锥,结合图像可知侧棱长为 ,而底面的边长为
,而底面的边长为 ,则根据正三棱锥的侧面与底面所成的二面角的余弦值是即为底面的高斜高的比值即为:O’D:VD即为
,则根据正三棱锥的侧面与底面所成的二面角的余弦值是即为底面的高斜高的比值即为:O’D:VD即为 ,故选A.
,故选A.
考点:本题主要是考查了折叠问题,解决此题的关键是抓住折叠前后不变的量解决问题,考查空间想象能力、运算能力和推理论证能力.
点评:解决该试题的关键是分析折叠图前后的不变量,以及得到的正三棱锥的底面的变长和侧棱长问题。

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
各棱长均为 的三棱锥的表面积为
的三棱锥的表面积为
A. | B. | C.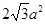 | D. |
若三棱锥的一条棱长为 ,其余棱长均为1,体积是
,其余棱长均为1,体积是 ,则函数
,则函数 在其定义域上为( )
在其定义域上为( )
| A.增函数且有最大值 | B.增函数且没有最大值 |
| C.不是增函数且有最大值 | D.不是增函数且没有最大值 |
对于一个底边在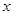 轴上的三角形,采用斜二测画法作出其直观图,其直观图面积是原三角形面积的 ( )
轴上的三角形,采用斜二测画法作出其直观图,其直观图面积是原三角形面积的 ( )
| A. 2倍 | B. 倍 倍 | C. 倍 倍 | D. 倍 倍 |
如图,在正方体 中,
中, 为
为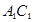 的中点,则异面直线
的中点,则异面直线 与
与 所成的角为( )
所成的角为( )
| A.30° | B.45° | C.60° | D.90 ° |
正方体 ,棱长为
,棱长为 ,点
,点 到截面
到截面 的距离为( )
的距离为( )
A. | B.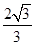 | C. | D. |
从点 出发的三条射线
出发的三条射线 两两成
两两成 角,且分别与球
角,且分别与球 相切于
相切于 三点,若球的体积为
三点,若球的体积为 ,则
,则 两点之间的距离为( )
两点之间的距离为( )
A. | B. | C.1.5 | D.2 |




 的棱长为
的棱长为 ,长为
,长为 的一个端点
的一个端点 在棱
在棱 上运动,点
上运动,点 在正方形
在正方形 内运动,则
内运动,则 的轨迹的面积为( )
的轨迹的面积为( )



