题目内容
2.求函数y=$\sqrt{2}$sin(2x+$\frac{π}{4}$),π∈[0,$\frac{π}{2}$]的值域.分析 求出相位的范围,然后求解函数的值域.
解答 解:x∈[0,$\frac{π}{2}$],可得:2x+$\frac{π}{4}$∈[$\frac{π}{4}$,$\frac{5π}{4}$],
函数y=$\sqrt{2}$sin(2x+$\frac{π}{4}$)∈[-1,$\sqrt{2}$].
函数的值域为:[-1,$\sqrt{2}$].
点评 本题考查三角函数的最值的求法,考查计算能力.

练习册系列答案
相关题目
12.设抛物线C:x2=4y的焦点为F,斜率为k的直线l经过点F,若抛物线C上存在四个点到直线l的距离为2,则k的取值范围是( )
| A. | (-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞) | B. | (-$\sqrt{3}$,-1)∪(1,$\sqrt{3}$) | C. | (-$\sqrt{3}$,$\sqrt{3}$) | D. | (-∞,-1)∪(1,+∞) |
10.四条直线每两条都相交,且任三条都不交于一点,它们可确定的平面个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.若函数f(x)=logsinα(x2-mx+3m)(α为锐角)在区间[2,+∞)上单凋递减,则实数m的取值围是( )
| A. | (0,4] | B. | (-4,4] | C. | (-∞,4] | D. | [4,+∞) |
14.如果平面α∥平面β,那么下列命题中不正确的是( )
| A. | 平面α内有无数条互相平行的直线平行于平面β | |
| B. | 平面α内仅有两条相交直线平行于平面β | |
| C. | 对于平面α内的任意一条直线,都能在平面β内找到一条直线与它平行 | |
| D. | 平面α内的任意一条直线都不与平面β相交 |
11.若$\frac{sinα+cosα}{cosα-sinα}$=tanβ,α,β∈[0,$\frac{π}{2}$),则β-α等于( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
8.已知幂函数f(x)=xa在[1,2]上的最大值与最小值的和为5,则α的值为( )
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | 3 |
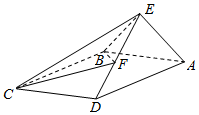 如图,在四棱锥E-ABCD中,底面ABCD是矩形,AB=2,AE⊥平面CDE,AE=DE=2$\sqrt{6}$,F为线段ED上的一点.
如图,在四棱锥E-ABCD中,底面ABCD是矩形,AB=2,AE⊥平面CDE,AE=DE=2$\sqrt{6}$,F为线段ED上的一点.