题目内容
如图,边长为2的正方形ABCD,E,F分别是AB,BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于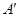
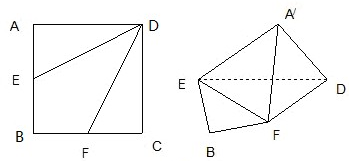
(1)求证: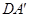 ⊥EF;
⊥EF;
(2)求
(1)见解析;(2)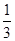
解析试题分析:(1)先根据正方形的特征得到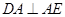 ,
,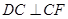 ,再根据点的重合得到
,再根据点的重合得到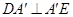 ,
,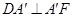 ,由直线与平面垂直的判定定理可知,
,由直线与平面垂直的判定定理可知,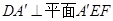 ,再由直线与平面垂直的性质定理得到
,再由直线与平面垂直的性质定理得到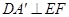 ;(2)先根据勾股定理求得
;(2)先根据勾股定理求得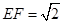 以及证明
以及证明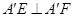 ,然后求得
,然后求得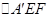 的面积,根据(1)中的
的面积,根据(1)中的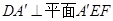 ,将三棱锥看作是以
,将三棱锥看作是以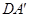 为高,以
为高,以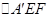 为底的几何体,那么求
为底的几何体,那么求 ,即是求
,即是求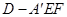 的体积,由
的体积,由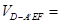
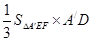 求解
求解
试题解析:(1)证明:∵ 是正方形,
是正方形,
∴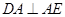 ,
,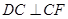 , 2分
, 2分
∴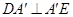 ,
,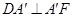 , 3分
, 3分
又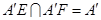 , 4分
, 4分
∴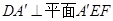 , 5分
, 5分
又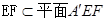 ,
,
∴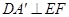 6分
6分
(2) 在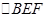 中,
中,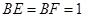 ,
,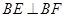 ,
,
∴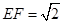 , 7分
, 7分
∵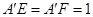 ,∴
,∴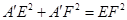 , 8分
, 8分
∴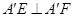 , 9分
, 9分
∴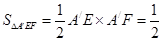 10分
10分
又由(1)知,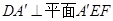 ,
,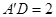
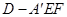 是三棱锥
是三棱锥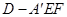 的高, 11分
的高, 11分
所以 
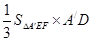 13分
13分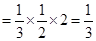 14分
14分
考点:1 直线与平面垂直的判定定理;2 直线与平面垂直的性质定理;3 解三角形;4 三棱锥的体积公式;5 勾股定理

练习册系列答案
相关题目
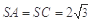 ,
,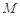 、
、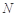 分别为
分别为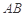 、
、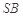 的中点.
的中点.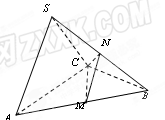
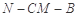 的余弦值;
的余弦值;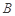 到平面
到平面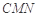 的距离.
的距离.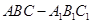 中,D、E分别为
中,D、E分别为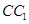 、AD的中点,F为
、AD的中点,F为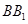 上的点,且
上的点,且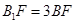
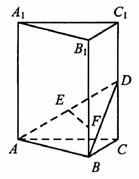
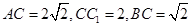 ,
,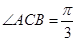 ,求二面角
,求二面角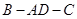 的大小.
的大小.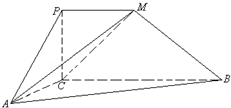

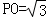 ,E、F分别是BC、AP的中点.
,E、F分别是BC、AP的中点.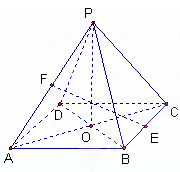
 的正方体截去一半(如图甲所示)得到如图乙所示的几何体,点
的正方体截去一半(如图甲所示)得到如图乙所示的几何体,点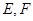 分别是
分别是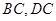 的中点.
的中点.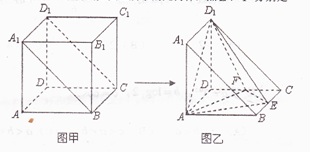
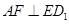 ;
;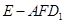 的体积.
的体积.
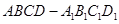 中,
中, ,点
,点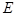 是
是 的中点.
的中点.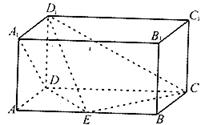
 的体积;
的体积; ;
; 的正切值.
的正切值.