题目内容
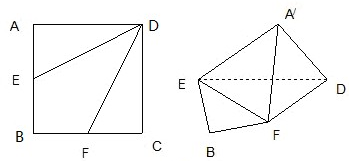
如图,在直三棱柱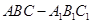 中,D、E分别为
中,D、E分别为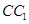 、AD的中点,F为
、AD的中点,F为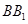 上的点,且
上的点,且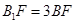
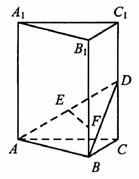
(I)证明:EF∥平面ABC;
(Ⅱ)若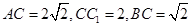 ,
,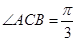 ,求二面角
,求二面角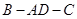 的大小.
的大小.
(I) EF∥平面ABC;(II) .
.
解析试题分析:(I) 取线段 的中点
的中点 ,证明平面
,证明平面 平面
平面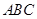 ,就可以证明
,就可以证明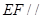 平面
平面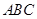 ;
;
(II)通过解 ,发现
,发现 ,又因为
,又因为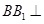 平面
平面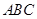 ,所以我们可以
,所以我们可以 为原点建立空间直角坐标系,求出平面
为原点建立空间直角坐标系,求出平面 和平面
和平面 的法向量的夹角,即为所求角或者是所求角的补角.
的法向量的夹角,即为所求角或者是所求角的补角.
试题解析:(I)取线段 的中点
的中点 ,并连接
,并连接 、
、 ,则
,则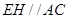 ,
, ,
,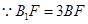
 ,
, ,
,
 平面
平面 平面
平面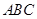 ,
, 平面
平面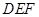 ,
,
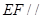 平面
平面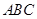
(II)已知在 中,
中, ,
,
由 ,可求得
,可求得

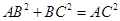

如图建立空间直角坐标系
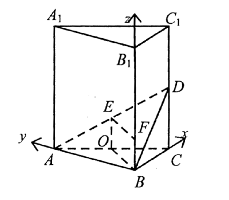
则 ,
, ,
,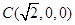 ,
,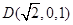 .
.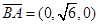 ,
, ,
,
设平面 的一个法向量
的一个法向量
则 ,即
,即
可取
设平面 的一个法向量
的一个法向量
则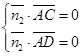 ,即
,即
可取

 二面角
二面角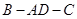 的大小为
的大小为
考点:1.线面平行的证明;2.空间直角坐标系的建立;3.法向量的求法;4.利用向量解决空间几何问题.

练习册系列答案
相关题目
 是一个斜三棱柱,已知
是一个斜三棱柱,已知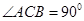 、平面
、平面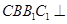 平面
平面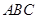 、
、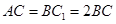 、
、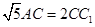 ,又
,又 、
、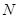 分别是
分别是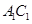 、
、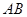 的中点.
的中点.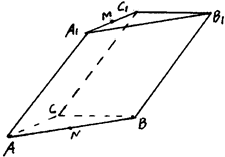
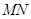 ∥平面
∥平面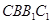 ; (2)求二面角
; (2)求二面角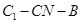 的大小.
的大小.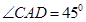 .
.
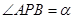 ,
, ,问点P在何处时,
,问点P在何处时,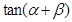 最小?
最小?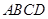 中,
中,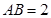 ,
,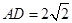 ,
,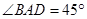 ,以
,以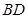 为折线,把
为折线,把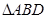 折起,使平面
折起,使平面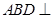 平面
平面 ,连结
,连结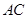 .
.
 ;
;  的大小.
的大小.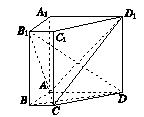
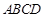 是菱形,
是菱形,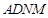 是矩形,平面
是矩形,平面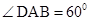 ,
,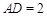 ,
,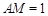 ,
,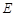 是
是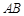 的中点.
的中点.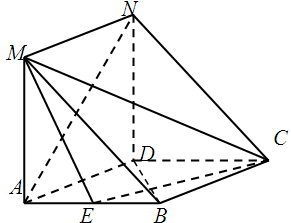
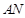 //平面
//平面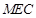 ;
;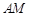 上是否存在点
上是否存在点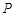 ,使二面角
,使二面角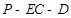 的大小为
的大小为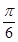 ?若存在,求出
?若存在,求出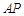 的长
的长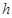 ;若不存在,请说明理由.
;若不存在,请说明理由.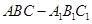 中,
中,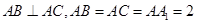 ,点
,点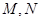 分别为
分别为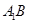 和
和 的中点.
的中点.
 平面
平面 ;
;
 ⊥EF;
⊥EF;
 中,四边形
中,四边形 是菱形,
是菱形, ,E为PB的中点.
,E为PB的中点.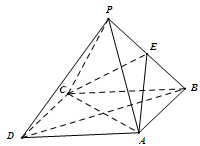
 平面
平面 ;
;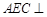 平面
平面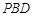 .
.