题目内容
13．下列四个命题：（1）y=1+x和y=$\sqrt{（1+x）^{2}}$表示相等函数；（2）函数f（x）在x＞0时是增函数，x＜0也是增函数，所以f（x）是增函数；
（3）f（x）=x2+2（a-1）x+2在区间（-∞，4]上是减函数，则实数a的取值范围是a≥-3；
（4）[-1，0]是y=x2-2|x|-3的一个递增区间．
其中正确命题的个数是（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 （1）根据函数的定义域，值域判断即可；
（2）根据单调性的定义判断即可；
（3）根据二次函数对称轴和单调性的关系判断即可；
（4）去绝对值，根据二次函数的单调性判断．
解答 解：（1）y=1+x的值域为R，y=$\sqrt{（1+x）^{2}}$的值域为[0，+∞），故不是相等函数，故错误；
（2）函数f（x）在x＞0时是增函数，x＜0也是增函数，只能说明有两个增区间，但但在整个区间上不一定是增函数，故错误；
（3）f（x）=x2+2（a-1）x+2在区间（-∞，4]上是减函数，则对称轴-$\frac{2（a-1）}{2}$≥4，得a≤-3，故错误；
（4）[-1，0]时，y=x2-2|x|-3=x2+2x-3，显然是一个递增区间，故正确．
故选B．
点评 考查了函数的概念，二次函数单调性的判断和绝对值函数的单调性，属于基础题型，应熟练掌握．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
8．定义在（-$\frac{π}{2}$，$\frac{π}{2}$）上的函数f（x）的导函数为f'（x），且当x∈（0，$\frac{π}{2}$）时，f'（x）＞sin2x•f（x）-cos2x•f'（x），若a=f（$\frac{π}{3}$），b=2f（0），c=$\sqrt{3}$f（$\frac{π}{6}$），则a，b，c的大小关系是（ ）
| A． | a＞b＞c | B． | c＞b＞a | C． | a＞c＞b | D． | b＞c＞a |
18．如图所示的程序框图中的错误是（ ）
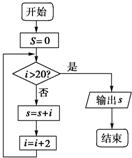
| A． | i没有赋值 | B． | 循环结构有错 | C． | s的计算不对 | D． | 判断条件不成立 |