题目内容
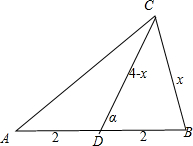
已知D是△ABC的边AB的中点，且AB=4，BC+CD=4，则△BCD面积的最大值为 ．
考点：三角形的面积公式
专题：解三角形
分析：设BC=x，则CD=4-x，记∠BDC=α，由余弦定理可得cosα=
，进而可得sinα=
，代入面积公式可得S=2
，由二次函数的最值可得．
| 5-2x |
| 4-x |
| ||
| 4-x |
| -3x2+12x-9 |
解答：
解：由题意可得AD=BD=2，设BC=x，则CD=4-x，记∠BDC=α
在△BCD中，由余弦定理可得x2=4+（4-x）2-4（4-x）cosα，
变形可得cosα=
，∴sinα=
=
，
∴△BCD面积S=2×
×2×（4-x）sinα=2
，
由二次函数的性质可知当x=-
=2时，上式取到最大值2
故答案为：2
在△BCD中，由余弦定理可得x2=4+（4-x）2-4（4-x）cosα，
变形可得cosα=
| 5-2x |
| 4-x |
| 1-cos2α |
| ||
| 4-x |
∴△BCD面积S=2×
| 1 |
| 2 |
| -3x2+12x-9 |
由二次函数的性质可知当x=-
| 12 |
| 2×(-3) |
| 3 |
故答案为：2
| 3 |
点评：本题考查三角形的面积公式，涉及余弦定理和二次函数的最值，属中档题．
练习册系列答案
相关题目
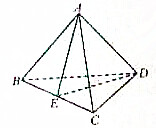在所有棱长均为2的四面体ABCD中，E是BC的中点，写出四面体中与平面AED垂直的面，并说明理由．