题目内容
已知函数 .
.
⑴求函数 在
在 处的切线方程;
处的切线方程;
⑵当 时,求证:
时,求证: ;
;
⑶若 ,且
,且 对任意
对任意 恒成立,求k的最大值.
恒成立,求k的最大值.
 .
.⑴求函数
 在
在 处的切线方程;
处的切线方程;⑵当
 时,求证:
时,求证: ;
;⑶若
 ,且
,且 对任意
对任意 恒成立,求k的最大值.
恒成立,求k的最大值.⑴ ;⑵详见解析;⑶
;⑵详见解析;⑶ 的最大值是3.
的最大值是3.
 ;⑵详见解析;⑶
;⑵详见解析;⑶ 的最大值是3.
的最大值是3.试题分析:⑴曲线
 在点
在点 处的切线方程为:
处的切线方程为: ,所以求出导数及切点即得切线方程;⑵不失一般性,左右两边作差得:
,所以求出导数及切点即得切线方程;⑵不失一般性,左右两边作差得:
 ,接下来用重要不等式比较真数的大小即可.⑶首先分离参数.由于
,接下来用重要不等式比较真数的大小即可.⑶首先分离参数.由于 ,所以
,所以 可变为
可变为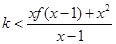 .令
.令 ,则
,则 ,注意到
,注意到 ,则
,则 取最大整数即可.接下来就利用导数求则
取最大整数即可.接下来就利用导数求则 的最小值.
的最小值.试题解析:⑴

∴故切线斜率

∴所切线方程:
 . .3分
. .3分⑵由题可知:


∵

∴

∴
 . 8分
. 8分⑶令

令
 在
在 上单调递增.
上单调递增.∵

∴所以
 存在唯一零点
存在唯一零点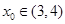 ,即
,即 .
.当
 时,
时, ;
;当
 时,
时, ;
;∴
 在
在 时单调递减;在
时单调递减;在 时,单调递增;
时,单调递增;∴

由题意
 ,又因为
,又因为 ,所以
,所以 的最大值是3. 14分
的最大值是3. 14分

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 ,
, (
( )
) 中的任意实数x,在
中的任意实数x,在 上总存在实数
上总存在实数 ,使得
,使得 成立,求实数
成立,求实数 的取值范围
的取值范围 ,当
,当 在区间
在区间 内变化时,
内变化时,
 的取值范围;
的取值范围;
 有零点,求实数m的最大值.
有零点,求实数m的最大值. 为函数
为函数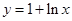 图象上一点,O为坐标原点,记直线
图象上一点,O为坐标原点,记直线 的斜率
的斜率 .
.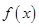 在区间
在区间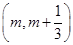
 上存在极值,求实数m的取值范围;
上存在极值,求实数m的取值范围;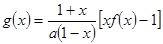 ,若对任意
,若对任意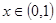 恒有
恒有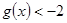 ,求实数
,求实数 的取值范围.
的取值范围. ,
, .
.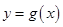 在点
在点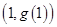 处的切线平行于
处的切线平行于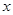 轴,求
轴,求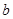 的值;
的值; 时,若对
时,若对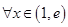 ,
,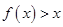 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,在(1)的条件下,证明当
,在(1)的条件下,证明当 时,对任意两个不相等的正数
时,对任意两个不相等的正数 、
、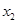 ,有
,有 .
.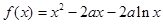 ,
,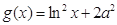 ,其中
,其中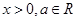 .
.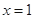 是函数
是函数 的极值点,求
的极值点,求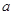 的值;
的值;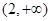 上单调递增,求
上单调递增,求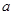 的取值范围;
的取值范围;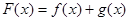 ,求证:
,求证: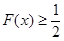 .
. 。
。 ,求
,求 在
在 处的切线方程;
处的切线方程; 的取值范围。
的取值范围。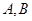 所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.

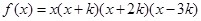 ,且
,且 ,则
,则 ( )
( )