题目内容
函数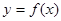 的定义域为
的定义域为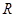 ,若存在常数
,若存在常数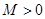 ,使得
,使得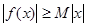 对一切实数
对一切实数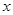 均成立,则称
均成立,则称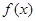 为“圆锥托底型”函数.
为“圆锥托底型”函数.
(1)判断函数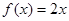 ,
,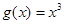 是否为“圆锥托底型”函数?并说明理由.
是否为“圆锥托底型”函数?并说明理由.
(2)若 是“圆锥托底型” 函数,求出
是“圆锥托底型” 函数,求出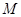 的最大值.
的最大值.
(3)问实数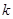 、
、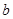 满足什么条件,
满足什么条件,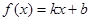 是“圆锥托底型” 函数.
是“圆锥托底型” 函数.
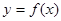 的定义域为
的定义域为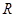 ,若存在常数
,若存在常数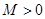 ,使得
,使得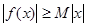 对一切实数
对一切实数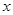 均成立,则称
均成立,则称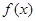 为“圆锥托底型”函数.
为“圆锥托底型”函数.(1)判断函数
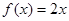 ,
,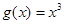 是否为“圆锥托底型”函数?并说明理由.
是否为“圆锥托底型”函数?并说明理由.(2)若
 是“圆锥托底型” 函数,求出
是“圆锥托底型” 函数,求出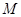 的最大值.
的最大值.(3)问实数
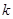 、
、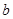 满足什么条件,
满足什么条件,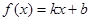 是“圆锥托底型” 函数.
是“圆锥托底型” 函数.(1)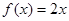 是,
是,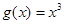 不是,(2)
不是,(2)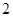 ,(3)
,(3)
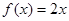 是,
是,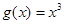 不是,(2)
不是,(2)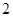 ,(3)
,(3)
试题分析:(1)新定义问题,必须读懂题意,严格按定义进行等价转化.本题判断函数是否为“圆锥托底型”函数,即判断是否存在常数
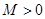 ,使得
,使得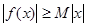 对一切实数
对一切实数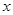 均成立,若成立必须证明,否则给出反例.本题解题关键在于常数
均成立,若成立必须证明,否则给出反例.本题解题关键在于常数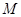 的确定.
的确定. 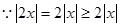 ,所以可确定常数
,所以可确定常数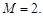 而由
而由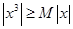 可知无论常数
可知无论常数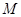 为什么正数,
为什么正数,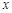 总能取较小的数比它小,即总能举个反例,如当
总能取较小的数比它小,即总能举个反例,如当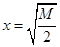 时,
时,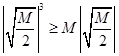 就不成立.(2)本题实质按新定义转化为不等式恒成立问题:存在
就不成立.(2)本题实质按新定义转化为不等式恒成立问题:存在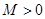 ,使得
,使得 对于任意实数恒成立.即当
对于任意实数恒成立.即当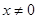 时,
时,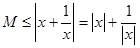 ,而
,而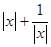 取得最小值2,
取得最小值2,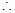
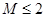 .(3)本题是讨论满足不等式恒成立的条件.即实数
.(3)本题是讨论满足不等式恒成立的条件.即实数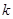 、
、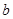 满足什么条件,存在常数
满足什么条件,存在常数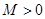 ,使得
,使得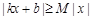 对一切实数
对一切实数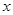 均成立.当
均成立.当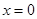 时,
时,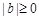 ,
,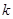 、
、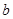 无限制条件;当
无限制条件;当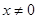 时,
时,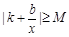 ,需
,需 ,否则若
,否则若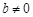 ,则当
,则当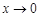 时,
时,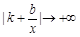 ,即
,即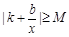 不能恒成立;若
不能恒成立;若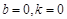 ,则
,则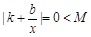 .
.试题解析:(1).
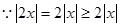 ,即对于一切实数
,即对于一切实数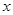 使得
使得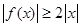 成立,
成立,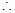
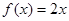 “圆锥托底型” 函数. 2分
“圆锥托底型” 函数. 2分对于
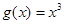 ,如果存在
,如果存在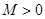 满足
满足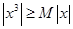 ,而当
,而当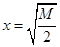 时,由
时,由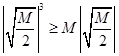 ,
,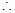
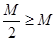 ,得
,得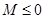 ,矛盾,
,矛盾,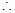
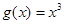 不是“圆锥托底型” 函数. 5分
不是“圆锥托底型” 函数. 5分(2)
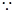
 是“圆锥托底型” 函数,故存在
是“圆锥托底型” 函数,故存在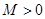 ,使得
,使得 对于任意实数恒成立.
对于任意实数恒成立.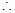 当
当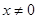 时,
时,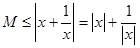 ,此时当
,此时当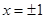 时,
时,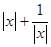 取得最小值2,
取得最小值2,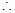
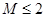 9分
9分而当
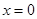 时,
时,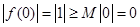 也成立.
也成立.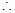
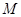 的最大值等于
的最大值等于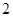 . 10分
. 10分(3)①当
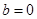 ,
,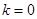 时,
时,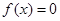 ,无论
,无论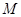 取何正数,取
取何正数,取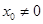 ,则有
,则有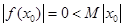 ,
,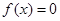 不是“圆锥托底型” 函数. 12分
不是“圆锥托底型” 函数. 12分②当
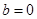 ,
,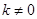 时,
时,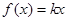 ,对于任意
,对于任意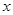 有
有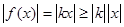 ,此时可取
,此时可取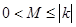
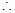
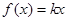 是“圆锥托底型” 函数. 14分
是“圆锥托底型” 函数. 14分③当
 ,
,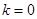 时,
时,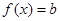 ,无论
,无论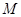 取何正数,取
取何正数,取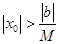 .有
.有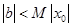 ,
,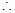
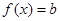 不是“圆锥托底型” 函数. 16分
不是“圆锥托底型” 函数. 16分④当
 ,
,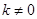 时,
时,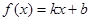 ,无论
,无论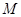 取何正数,取
取何正数,取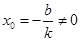 ,有
,有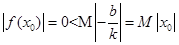 ,
,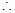
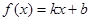 不是“圆锥托底型” 函数.
不是“圆锥托底型” 函数.由上可得,仅当
 时,
时,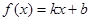 是“圆锥托底型” 函数. 18分
是“圆锥托底型” 函数. 18分
练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
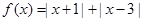 .
.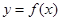 的图像;
的图像;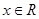 ,
,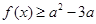 恒成立,求实数
恒成立,求实数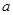 的取值范围.
的取值范围.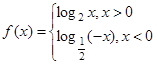 ,若
,若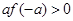 ,则实数
,则实数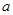 的取值范围是( )
的取值范围是( )
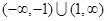
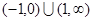
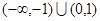
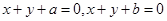 ,已知
,已知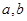 是方程
是方程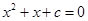 的两个实根,且
的两个实根,且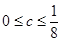 ,则这两条直线之间的距离的最大值和最小值分别是( )
,则这两条直线之间的距离的最大值和最小值分别是( )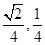
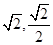
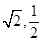
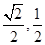
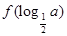 ≤2f(1),则a的取值范围是 ( )
≤2f(1),则a的取值范围是 ( )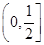
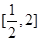
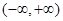 的奇函数
的奇函数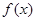 为增函数,偶函数
为增函数,偶函数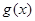 在区间
在区间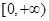 的图象与
的图象与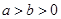 ,给出下列不等式:
,给出下列不等式: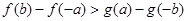 ②
②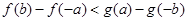
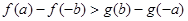 ④
④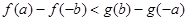 其中成立的是( )
其中成立的是( )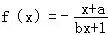 为区间[﹣1,1]上的奇函数,则它在这一区间上的最大值是.
为区间[﹣1,1]上的奇函数,则它在这一区间上的最大值是.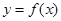 是定义域为
是定义域为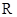 的偶函数. 当
的偶函数. 当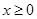 时,
时,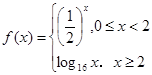 若关于
若关于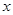 的方程
的方程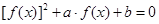
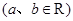 有且只有7个不同实数根,则实数
有且只有7个不同实数根,则实数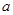 的取值范围是 .
的取值范围是 .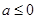 ”是“函数
”是“函数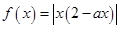 在区间
在区间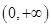 内单调递增”的( )
内单调递增”的( )