题目内容
“
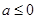”是“函数
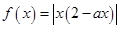在区间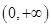
内单调递增”的（ ）
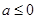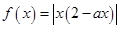”是“函数在区间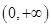内单调递增”的（ ）| A．充分不必要条件 | B．必要不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
C
试题分析：当
时，
，此时函数
在区间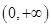内单调递增，当
时，令
，解得
或
，当
时，结合图象可知，函数在区间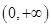内单调递增，当
时，结合图象可知，函数在区间
上单调递增，在区间
上单调递减，在区间
上单调递增，不合乎题意！因此“
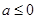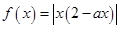”是“函数在区间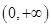内单调递增”的充分必要条件，故选C.
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
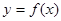的定义域为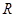
，若存在常数
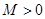，使得
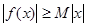对一切实数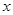
均成立，则称
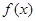为“圆锥托底型”函数．
，
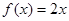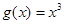是否为“圆锥托底型”函数？并说明理由．
是“圆锥托底型” 函数，求出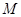
的最大值．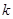
、
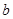满足什么条件，
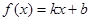是“圆锥托底型” 函数．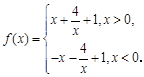
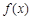的奇偶性；
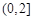和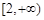
上的增减性；
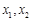满足：
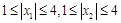，试证明：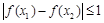
．
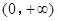内单调递减，并且是偶函数的是（ ）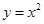
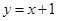
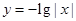
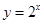
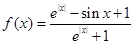在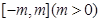
上的最大值为p，最小值为q，则p+q= 
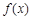是定义在R上的偶函数, 且在区间
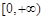单调递增．若实数
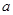满足
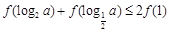,则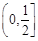
.
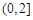
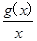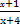)的所有x之和为( )
