题目内容
设数列{an}的前n项和为Sn,数列{Sn}的前n项和为Tn,满足Tn=2Sn-n2,n∈N*.
(1)求a1的值;
(2)求数列{an}的通项公式.
【解】 (1)当n=1时,T1=2S1-12.
因为T1=S1=a1, 所以a1=2a1-1,解得a1=1.
所以a1=2a1-1,解得a1=1.
(2)当n≥2时,Sn=Tn-Tn-1=2Sn-n2-[2Sn-1-(n-1)2]=2Sn-2Sn-1-2n+1,
所以Sn=2Sn-1+2n-1,①
所以Sn+1=2Sn+2n+1,②
②-①得an+1=2an+2.
所以an+1+2=2(an+2),即
当n=1时,a1+2=3,a2+2=6,则 ,所以当n=1时也满足上式.所以{an+2}是以3为首项,2为公比的等比数列,所以an+2=3·2n-1,所以an=3·2n-1-2.
,所以当n=1时也满足上式.所以{an+2}是以3为首项,2为公比的等比数列,所以an+2=3·2n-1,所以an=3·2n-1-2.

练习册系列答案
相关题目
 中,已知
中,已知 是边长为1的正方形,且
是边长为1的正方形,且 是正三角形,,
是正三角形,, ,则该多面体的体积为
,则该多面体的体积为 ( )
( ) (B)
(B)  (C)
(C)  (D)
(D)

 =
= ,则
,则 =________.
=________.

 其中e是自然常数,
其中e是自然常数,
 时,
时,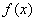 的单调性、极值;
的单调性、极值; .
. 函数f(x)=(1-cos x)sin x在[-π,π]的图象大致为( )
函数f(x)=(1-cos x)sin x在[-π,π]的图象大致为( ) 确定的平面区域记为Ω1,不
确定的平面区域记为Ω1,不 等式组
等式组 确定的平面区域记为Ω2,在Ω1中随机取一点,则该点恰好在Ω2内的概率为( )
确定的平面区域记为Ω2,在Ω1中随机取一点,则该点恰好在Ω2内的概率为( )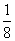 B.
B. C.
C. D.
D.

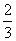 ,若函数f(x)=x3+1在点(1,f(1))处的切线过点(an+1,an).
,若函数f(x)=x3+1在点(1,f(1))处的切线过点(an+1,an).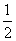 }为等比数列;
}为等比数列;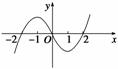 设f(x)是一个三次函数,f′(x)为其导函数,如图所示的是y=x·f′(x)的图象的一部分,则f(x)的极大值与极小值分别是( )
设f(x)是一个三次函数,f′(x)为其导函数,如图所示的是y=x·f′(x)的图象的一部分,则f(x)的极大值与极小值分别是( )