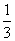题目内容
在数列{an}中，a1＝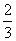
，若函数f(x)＝x3＋1在点(1，f(1))处的切线过点(an＋1，an)．
(1)求证：数列{an－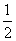
}为等比数列；
(2)求数列{an}的通项公式和前n项和公式Sn.
【解】 (1)证明 因为f′(x)＝3x2，所以切线的斜率为k＝3，切点是(1,2)，切线方程为y－2＝3(x－1)⇒3x－y－1＝0，又因为过点(an＋1，an)，所以3an＋1－an－1＝0，即3an＋1＝an＋1所以3an＋1－
＝an－⇒
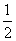即数列{an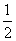－}为等比数列，其中公比q＝
.
(2)由(1)得{an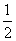－}为公比为q＝，首项a1－＝－＝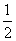
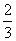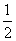的等比数列，则an－
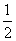＝·()n－1，
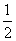∴an＝·()n＋，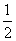
Sn＝(＋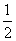
＋…＋
)＋
练习册系列答案
相关题目
，则这个椭圆的焦距为( )
C．
D．
如果存在实数
使得对任意实数x，都有
则
的最小值是____.
B．
D．
为数列
的前n项和，
则(1)
_ ___；
__ _.．, 
，则f(2＋log23)的值为( )
B.
C.
D.