题目内容
20.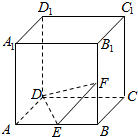 如图,正方体ABCD-A1B1C1D1中,E,F分别为AB与BB1的中点.
如图,正方体ABCD-A1B1C1D1中,E,F分别为AB与BB1的中点.(Ⅰ)求证:EF⊥平面A1D1B;
(Ⅱ)求二面角F-DE-C大小.
分析 (I)要证EF⊥平面A1D1B,只需证A1D1⊥EF,A1B⊥EF
(II)要求二面角F-DE-C大小的正切值,关键是找出二面角的平面角.延长DE、CB交于N,过B作BM⊥EN交于M,连FM,则∠FMB为二面角F-DE-C的平面角,故可求.
解答 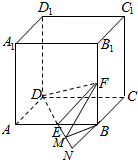 证明:(I)∵A1D1⊥平面A1B1BA,EF?平面A1B1BA,
证明:(I)∵A1D1⊥平面A1B1BA,EF?平面A1B1BA,
∴A1D1⊥EF
∵A1B⊥AB1,EF∥AB1,
∴A1B⊥EF
∴EF⊥平面A1D1B;
解:(II)延长DE、CB交于N,∵E为AB中点,∴△DAE≌△NBE
过B作BM⊥EN交于M,连FM,
∵FB⊥平面ABCD
∴FM⊥DN,∴∠FMB为二面角F-DE-C的平面
设AB=a,则BM=$\frac{BE•BN}{EN}$=$\frac{a}{\sqrt{5}}$ 又BF=$\frac{a}{2}$,
∴tan∠FMB=$\frac{FB}{BM}$=$\frac{\sqrt{5}}{2}$,
即二面角F-DE-C大小为:arctan$\frac{\sqrt{5}}{2}$.
点评 本题以正方体为载体,考查线面垂直,考查面面角,关键是作出二面角的平面角.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
8.已知b2-4ac是一元二次方程ax2+bx+c=0(a≠0)的一个实数根,则( )
| A. | ab≤$\frac{1}{8}$ | B. | ab≥$\frac{1}{8}$ | C. | ab$≥\frac{1}{4}$ | D. | ab$≤\frac{1}{4}$ |
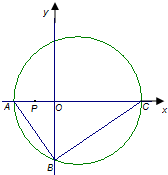 如图,直角三角形ABC的顶点坐标A(-2,0),直角顶点$B(0,-2\sqrt{2})$,顶点C在x轴上,点P为线段OA的中点.
如图,直角三角形ABC的顶点坐标A(-2,0),直角顶点$B(0,-2\sqrt{2})$,顶点C在x轴上,点P为线段OA的中点. 如图,点P为⊙O外一点,过点P作⊙O的两条切线,切点分别为A、B.过点A作PB的平行线,交⊙O于点C,连接PC,交⊙O于点E;连接AE,并延长AE交PB于点E,求证:PE•AC=CE•KB.
如图,点P为⊙O外一点,过点P作⊙O的两条切线,切点分别为A、B.过点A作PB的平行线,交⊙O于点C,连接PC,交⊙O于点E;连接AE,并延长AE交PB于点E,求证:PE•AC=CE•KB.