题目内容
8.已知圆C的圆心为点C(0,3),点R($\sqrt{3}$,2)在圆C上,直线l过点A(-1,0)且与圆C相交P,Q两点,点M是线段PQ的中点.(1)求圆C的方程:
(2)若$\overrightarrow{AM}$•$\overrightarrow{AC}$=9,求直线l的方程.
分析 (1)利用两点间距离公式可求出圆C的半径,进而可得结论;
(2)通过设直线l的方程为:y=k(x+1),利用△ACM为直角三角形,化简可知${\overrightarrow{AM}}^{2}$=9,进而利用点到直线的距离公式及勾股定理计算即得结论.
解答 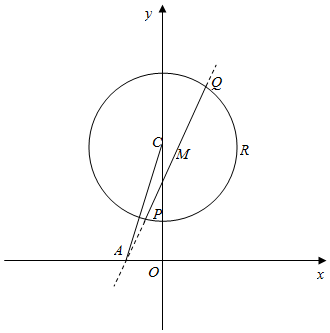 解:(1)∵圆C的圈心为点C(0,3),点R($\sqrt{3}$,2)在圆C上,
解:(1)∵圆C的圈心为点C(0,3),点R($\sqrt{3}$,2)在圆C上,
∴圆C的半径r=|CR|=$\sqrt{(\sqrt{3}-0)^{2}+(2-3)^{2}}$=2,
∴圆C的方程为:x2+(y-3)2=4;
(2)依题意,设直线l的方程为:y=k(x+1),
∵点M是线段PQ的中点,
∴CM⊥PQ,且△ACM为直角三角形,
又∵$\overrightarrow{AM}$•$\overrightarrow{AC}$=$\overrightarrow{AM}$•($\overrightarrow{AM}$+$\overrightarrow{MC}$)=${\overrightarrow{AM}}^{2}$=9,
∴AM=3,
∵CM=$\frac{|0-3+k|}{\sqrt{1+{k}^{2}}}$,AC=$\sqrt{(-1-0)^{2}+(0-3)^{2}}$=$\sqrt{10}$,
∴AC2=CM2+AM2,即10=$\frac{(3-k)^{2}}{1+{k}^{2}}$+9,
解得:k=$\frac{4}{3}$,
从而直线l的方程为y=$\frac{4}{3}$(x+1).
点评 本题考查直线与圆的方程的应用,考查数形结合能力,涉及点到直线的距离公式、两点间距离公式、勾股定理等基础知识,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
20.若直线经过抛物线y2=4x的焦点且与抛物线相交于M、N两点,且线段MN中点的横坐标为3,则线段MN的长为( )
| A. | $\sqrt{13}$ | B. | 8 | C. | $8\sqrt{2}$ | D. | 16 |
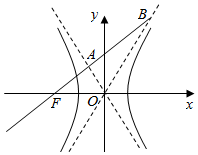 如图,已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左焦点为F,过F作斜率为1的直线交双曲线的渐近线于A,B两点,且|OB|=2|OA|,则该双曲线的离心率为$\sqrt{10}$.
如图,已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左焦点为F,过F作斜率为1的直线交双曲线的渐近线于A,B两点,且|OB|=2|OA|,则该双曲线的离心率为$\sqrt{10}$.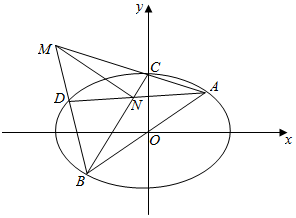 如图,在平面直角坐标系xOy中,椭圆E的方程为$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,直线l:y=$\frac{1}{2}$x与椭圆E相交于A,B两点,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N,求证:直线MN的斜率为定值.
如图,在平面直角坐标系xOy中,椭圆E的方程为$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,直线l:y=$\frac{1}{2}$x与椭圆E相交于A,B两点,C,D是椭圆E上异于A,B两点,且直线AC,BD相交于点M,直线AD,BC相交于点N,求证:直线MN的斜率为定值.