题目内容
已知椭圆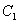 :
: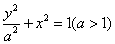 与抛物线
与抛物线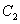 :
: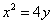 有相同焦点
有相同焦点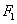 .
.
(Ⅰ)求椭圆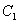 的标准方程;
的标准方程;
(Ⅱ)已知直线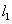 过椭圆
过椭圆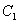 的另一焦点
的另一焦点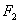 ,且与抛物线
,且与抛物线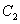 相切于第一象限的点
相切于第一象限的点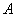 ,设平行
,设平行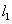 的直线
的直线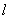 交椭圆
交椭圆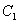 于
于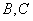 两点,当△
两点,当△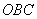 面积最大时,求直线
面积最大时,求直线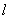 的方程.
的方程.
(Ⅰ)由于抛物线 的焦点为
的焦点为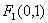 ,得到
,得到 ,又
,又 得到
得到 .
.
(Ⅱ)思路一:设 ,
, ,
,
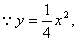


 直线
直线 的方程为
的方程为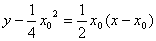 即
即 且过点
且过点
 ,
,
 切线
切线 方程为
方程为
由 ,设直线
,设直线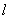 的方程为
的方程为 ,联立方程组
,联立方程组
由 ,消
,消 整理得
整理得

设 ,
, ,应用韦达定理
,应用韦达定理 
得
 ,由点
,由点 到直线
到直线 的距离为
的距离为 ,
,
 应用基本不等式等号成立的条件求得
应用基本不等式等号成立的条件求得
思路二: ,由已知可知直线
,由已知可知直线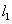 的斜率必存在,设直线
的斜率必存在,设直线
由 消去
消去 并化简得
并化简得
根据直线 与抛物线
与抛物线 相切于点
相切于点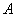 .得到
.得到 ,
, .
.
根据切点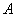 在第一象限得
在第一象限得 ;由
;由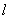 ∥
∥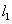 ,设直线
,设直线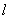 的方程为
的方程为
由 ,消去
,消去 整理得
整理得 , 思路同上.
, 思路同上.
试题解析:(Ⅰ) 抛物线
抛物线 的焦点为
的焦点为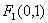 ,
,
 ,又
,又
 椭圆方程为
椭圆方程为 . 4分
. 4分
(Ⅱ)(法一)设 ,
, ,
,
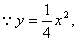
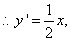

 直线
直线 的方程为
的方程为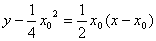 即
即 且过点
且过点
 ,
,
 切线
切线 方程为
方程为 6分
6分
因为 ,所以设直线
,所以设直线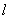 的方程为
的方程为 ,
,
由 ,消
,消 整理得
整理得 7分
7分
 ,解得
,解得 ①
①
设 ,
, ,则
,则

∴
 8分
8分
直线 的方程为
的方程为 ,
,
 点
点 到直线
到直线 的距离为
的距离为 9分
9分
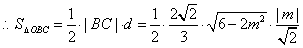
 , 10分
, 10分
由① ,
, 
 (当且仅当
(当且仅当 即
即 时,取等号)
时,取等号)
 最大
最大
所以,所求直线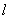 的方程为:
的方程为: . 12分
. 12分

(法二) ,由已知可知直线
,由已知可知直线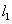 的斜率必存在,
的斜率必存在,
设直线
由 消去
消去 并化简得
并化简得
∵直线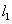 与抛物线
与抛物线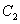 相切于点
相切于点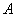 .
.
∴ ,得
,得 . 5分
. 5分
∵切点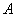 在第一象限.
在第一象限.
∴ 6分
6分
∵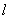 ∥
∥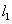
∴设直线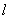 的方程为
的方程为
由 ,消去
,消去 整理得
整理得 , 7分
, 7分
 ,解得
,解得 .
.
设 ,
, ,则
,则
 ,
,
 . 8分
. 8分
又直线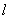 交
交 轴于
轴于
 10分
10分

当 ,即
,即 时,
时, . 11分
. 11分
所以,所求直线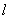 的方程为
的方程为 . 12分
. 12分
考点:1.椭圆、抛物线标准方程及几何性质;2.直线与圆锥曲线的位置关系.

 的图象向右平移三个单位长度得到图象
的图象向右平移三个单位长度得到图象 ,再将图象
,再将图象 倍(纵坐标不变)得到图象
倍(纵坐标不变)得到图象 ,则
,则 ,如果
,如果 是
是 的充分不必要条件,则实数
的充分不必要条件,则实数 的取值范围是( )
的取值范围是( )  B.
B. C.
C. D.
D.
 焦点的直线
焦点的直线 的倾斜角为
的倾斜角为 ,且
,且 两点,
两点, 的面积为 .
的面积为 . 在点
在点 处的切线的倾斜角是( )
处的切线的倾斜角是( ) B.45
B.45 的焦点为
的焦点为 ,不经过焦点的直线上有三个不同的点
,不经过焦点的直线上有三个不同的点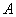 ,
, ,
, ,其中点
,其中点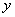 轴上,则
轴上,则 与
与 的面积之比是( )
的面积之比是( )
 B.
B. C.
C. D.
D.

 的值;
的值; 的值
的值 的部分图象如图所示.
的部分图象如图所示.
 的解析式;
的解析式; ,求
,求 的值.
的值.