题目内容
在数列{an}中,a1=1,3anan-1+an-an-1=0(n≥2).
(1)证明数列 是等差数列;
是等差数列;
(2)求数列{an}的通项;
(3)若λan+ ≥λ对任意n≥2的整数恒成立,求实数λ的取值范围.
≥λ对任意n≥2的整数恒成立,求实数λ的取值范围.
解:(1)证明:将3anan-1+an-an-1=0(n≥2)整理得 =3(n
=3(n ≥2).
≥2).
所以数列 是以1为首项,3为公差的等差数列.
是以1为首项,3为公差的等差数列.
(2)由(1)可得 =1+3(n-1)=3n-2,所以an=
=1+3(n-1)=3n-2,所以an= .
.
 因为n≥2,所以cn+1-cn>0,即数列{cn}为单调递增数列,所以c2最小,c2=
因为n≥2,所以cn+1-cn>0,即数列{cn}为单调递增数列,所以c2最小,c2= .
.
所以λ的取值范围为 .
.

练习册系列答案
相关题目


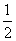 an-30,求数列{bn}的前n项和的最小值.
an-30,求数列{bn}的前n项和的最小值. ,求函数y=4x(3-2x)的最大值;
,求函数y=4x(3-2x)的最大值; 知x,y都是正实数,且x+y-3xy+5=0,求xy的最小值.
知x,y都是正实数,且x+y-3xy+5=0,求xy的最小值.