题目内容
20.已知函数f(x)=(x+a)(|x|+2)+b(a,b∈R)(1)若f(x)在R上不单调,求实数a的取值范围;
(2)若a≤-4且y=f(x)在[-1,1]上有两个零点,求a2+(b-17)2的最小值.
分析 (1)由函数f(x)去掉绝对值,得f(x)=$\left\{\begin{array}{l}{{x}^{2}+(2+a)x+2a+b,x≥0}\\{-{x}^{2}+(2-a)x+2a+b,x≤0}\end{array}\right.$,又由f(x)在R上不单调,列出不等式组求解即可得答案;
(2)由f(x)=$\left\{\begin{array}{l}{{x}^{2}+(2+a)x+2a+b,x≥0}\\{-{x}^{2}+(2-a)x+2a+b,x≤0}\end{array}\right.$,若a≤-4且y=f(x)在[-1,1]上有两个零点,且$-\frac{2+a}{2}≥1$,可得$\left\{\begin{array}{l}{f(-1)≤0}\\{f(0)>0}\\{f(1)≤0}\end{array}\right.$,再由线性规划可得答案.
解答 解:(1)由函数f(x)=(x+a)(|x|+2)+b(a,b∈R),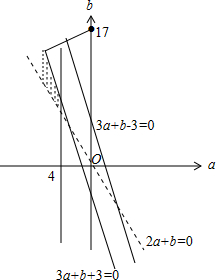
得f(x)=$\left\{\begin{array}{l}{{x}^{2}+(2+a)x+2a+b,x≥0}\\{-{x}^{2}+(2-a)x+2a+b,x≤0}\end{array}\right.$,
若f(x)在R上不单调,
得$-\frac{2+a}{2}>0$或$\frac{2-a}{2}<0$,
实数a的取值范围为:a<-2或a>2;
(2)f(x)=$\left\{\begin{array}{l}{{x}^{2}+(2+a)x+2a+b,x≥0}\\{-{x}^{2}+(2-a)x+2a+b,x≤0}\end{array}\right.$,
若a≤-4且y=f(x)在[-1,1]上有两个零点,且$-\frac{2+a}{2}≥1$,
则$\left\{\begin{array}{l}{f(-1)≤0}\\{f(0)>0}\\{f(1)≤0}\end{array}\right.$,即$\left\{\begin{array}{l}{3a+b-3≤0}\\{2a+b>0}\\{3a+b+3≤0}\\{a≤-4}\end{array}\right.$,
a2+(b-17)2的几何意义为定点(0,17)
与可行域内动点距离的平方,
由$\frac{|3×0+1×17+3|}{\sqrt{10}}=2\sqrt{10}$,
得a2+(b-17)2的最小值为$(2\sqrt{10})^{2}$=40.
点评 本题考查了二次函数的性质,考查了函数零点的判定以及简单线性规划知识,体现了数形结合的解题思想方法,是中档题.

| A. | (0,1) | B. | (-∞,0)∪(0,1) | C. | (-∞,0)∪(0,2) | D. | (-1,0)∪(0,1) |
| A. | 1 | B. | $\frac{1}{4}$ | C. | $-\frac{1}{4}$ | D. | -1 |
