题目内容
已知O是空间任意一点,A、B、C、D四点满足任三点均不共线,但四点共面,且
=2x•
+3y•
+4z•
,则2x+3y+4z=
| OA |
| BO |
| CO |
| DO |
-1
-1
.分析:利用空间向量基本定理,及向量共面的条件,即可得到结论.
解答:解:∵
=2x•
+3y•
+4z•
,
∴
=-2x•
-3y•
-4z•
,
∵O是空间任意一点,A、B、C、D四点满足任三点均不共线,但四点共面
∴-2x-3y-4z=1
∴2x+3y+4z=-1
故答案为:-1
| OA |
| BO |
| CO |
| DO |
∴
| OA |
| OB |
| OC |
| OD |
∵O是空间任意一点,A、B、C、D四点满足任三点均不共线,但四点共面
∴-2x-3y-4z=1
∴2x+3y+4z=-1
故答案为:-1
点评:本题考查空间向量基本定理,考查向量共面的条件,属于基础题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 ,则3x+4y+5z=________.
,则3x+4y+5z=________. =2x•
=2x• +3y•
+3y•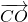 +4z•
+4z• ,则2x+3y+4z=________.
,则2x+3y+4z=________.