题目内容
已知O是空间任意一点,P∈平面ABC,且| OP |
| 1 |
| 5 |
| OA |
| 2 |
| 5 |
| OB |
| OC |
分析:利用四点共面的充要条件,列出方程求出x.
解答:解:∵
=
+
+x
又P∈平面ABC
∴
+
+x=1
解得x=
故答案为:
| OP |
| 1 |
| 5 |
| OA |
| 2 |
| 5 |
| OB |
| OC |
又P∈平面ABC
∴
| 1 |
| 5 |
| 2 |
| 5 |
解得x=
| 2 |
| 5 |
故答案为:
| 2 |
| 5 |
点评:本题考查四点共面的充要条件:P∈平面ABC,若
=
+y
+z
则x+y+z=1
| OP |
| xOA |
| OB |
| OC |

练习册系列答案
相关题目
 ,则3x+4y+5z=________.
,则3x+4y+5z=________. =2x•
=2x• +3y•
+3y•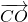 +4z•
+4z• ,则2x+3y+4z=________.
,则2x+3y+4z=________.