题目内容
11.过抛物线y2=2px(p>0)的焦点F作直线交抛物线于A,B,若S△OAF=3S△OBF,则直线AB的斜率为( )| A. | $±\frac{{\sqrt{3}}}{3}$ | B. | $±\frac{4}{3}$ | C. | $±\sqrt{3}$ | D. | $±\frac{3}{4}$ |
分析 据S△AOF=3S△BOF,得|AF|=3|BF|,得$\overrightarrow{AF}$=3$\overrightarrow{BF}$,求得-y1=3y2,设出直线AB的方程,与抛物线方程联立消去x,利用韦达定理求出斜率,即可求出tanα.
解答 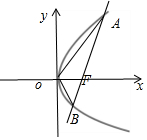 解:根据题意设点A(x1,y1),B(x2,y2).
解:根据题意设点A(x1,y1),B(x2,y2).
由S△AOF=3S△BOF,得|AF|=3|BF|,得$\overrightarrow{AF}$=3$\overrightarrow{BF}$,得($\frac{p}{2}$-x1,-y1)=3($\frac{p}{2}$-x2,-y2),
故-y1=3y2,即$\frac{{y}_{1}}{{y}_{2}}$=-3.
设直线AB的方程为y=k(x-$\frac{p}{2}$).联立$\left\{\begin{array}{l}{y=k(x-\frac{p}{2})}\\{y=2px}\end{array}\right.$,消元得ky2-2py-kp2=0.
故y1+y2=$\frac{2p}{k}$,y1y2=-p2.则$\frac{({y}_{1}+{y}_{2})^{2}}{{y}_{1}{y}_{2}}$=$\frac{{y}_{1}}{{y}_{2}}$+$\frac{{y}_{2}}{{y}_{1}}$+2=-$\frac{4}{3}$,-$\frac{4}{{k}^{2}}$=-$\frac{4}{3}$,解得k=$\sqrt{3}$,
即直线AB的斜率为±$\sqrt{3}$,
故选:C
点评 本题主要考查了抛物线的概念和性质,直线和抛物线的综合问题,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
1.函数y=x-2,y=2x2,y=(x+1)2,y=3x中,幂函数的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
2.已知x,y满足$\left\{\begin{array}{l}{x-y≥0}\\{x+y-4≥0}\\{x≤4}\end{array}\right.$,则z=4x+y的最小值为( )
| A. | 6 | B. | 8 | C. | 10 | D. | 15 |
19.在△ABC中tanA+tanB=1-tanAtanB则∠A+∠B等于( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
6.已知函数f(x)满足f(-x)=f(x)和f(x+2)=f(x),且当x∈[0,1]时,f(x)=1-x,则函数g(x)=f(x)-($\frac{1}{3}$)x在x∈[-4,4]上零点的个数是( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
20.已知$tanα=\frac{1}{2}$,则$\frac{sinαcosα}{{{{sin}^2}α-co{s^2}α}}$的值是( )
| A. | $-\frac{4}{3}$ | B. | 3 | C. | $\frac{4}{3}$ | D. | $-\frac{2}{3}$ |
1.角-870°的终边所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |