题目内容

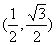 已知向量a = ,b =,且存在实数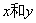,使向量m = a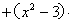b, n = a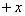b,且m⊥n．

  (Ⅰ)求函数的关系式,并求其单调区间和极值；

  (Ⅱ)是否存在正数Ｍ,使得对任意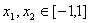,都有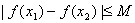成立?若存在求出M；若不存在,说明理由．

 

 

 

 

 

 

 

 

 

【答案】

 解（Ⅰ）a·b ＝ 0，m⊥n ，m·n =[ab]·（ ab）

   = a2b2 == 0，．

　　，在为增函数，

　　在为减函数．

　　的极大值为，的极小值为．

　　（Ⅱ）在［1,1］上为减函数,,

    对任意,都有,

    故存在正数Ｍ符合要求．

练习册系列答案
相关题目
已知向量
a
，
b
满足|
a
|=1，|
b
|=2，且
a
与
b
方向上的投影与
b
在
a
方向上的投影相等，则|
a
-
b
|等于（　　）
A、3
B、
5
C、
3
D、1
已知向量
a
，
b
满足
a
=(x，2)，
b
=(1，-3)，且（2
a
+
b
）⊥
b
．
（1）求向量
a
的坐标；     
（2）求向量
a
与
b
的夹角．
给出下列四个命题：
①如果命题“?p”与命题“p或q”都是真命题，那么命题q一定是真命题；
②已知向量
a
，
b
满足|
a
|=1，|
b
|=4，且
a
•
b
=2，则
a
与
b
的夹角为
π
6
；
③若函数f（x+1）是奇函数，f（x-1）是偶函数，且f（0）=2，则f（2012）=2；
④已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数，函数g(x)=log4(a•2x-
4
3
a)，若函数f（x）的图象与函数g（x）的图象有且只有一个公共点，则实数a的取值范围是（1，+∞）．
其中正确命题的序号为
①
①
．
已知向量
a
，
b
，
c
满足
a
+
b
+
c
=0，且
a
与
c
的夹角为60°，|b|=
3
|a|，则tan＜
a
，
b
≥（　　）
已知向量
a
，
b
，且|
a
|=1，|
b
|=2，则|2
b
-
a
|的取值范围是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网