题目内容
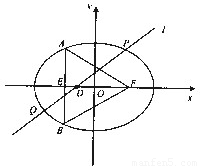
设点O,F分别是原点和抛物线y2=4x的焦点,抛物线上的点A在其准线上的射影为B,且∠OFB=60°,则△ABF的面积为( )
分析:作出函数的图象,可判断△ABF为边长是4的等边三角形,从而可求其面积.
解答: 解:依题意,作图如图:
解:依题意,作图如图:
∵y2=4x的焦点F(1,0),准线方程为:x=-1,设准线与x轴的交点为M,
在Rt△BFM中,∠OFB=60°,|MF|=2,
∴|BF|=4,
又AB∥x轴,
∴∠ABF=60°,
由抛物线的定义得:|AB|=|AF|,
∴△ABF为边长是4的等边三角形,
∴S△ABF=
×4×4×
=4
.
故选C.
 解:依题意,作图如图:
解:依题意,作图如图:∵y2=4x的焦点F(1,0),准线方程为:x=-1,设准线与x轴的交点为M,
在Rt△BFM中,∠OFB=60°,|MF|=2,
∴|BF|=4,
又AB∥x轴,
∴∠ABF=60°,
由抛物线的定义得:|AB|=|AF|,
∴△ABF为边长是4的等边三角形,
∴S△ABF=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
故选C.
点评:本题考查抛物线的简单性质,考查转化思想与数形结合思想,考查运算能力,属于中档题.

练习册系列答案
相关题目
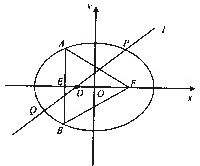 (2012•九江一模)设点E、F分别是椭圆C:
(2012•九江一模)设点E、F分别是椭圆C:


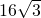
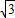
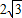
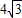
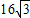
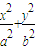 =1(a>b>0)的左、右焦点,过点E垂直于椭圆长轴的直线交椭圆于A、B两点,△ABF是正三角形.
=1(a>b>0)的左、右焦点,过点E垂直于椭圆长轴的直线交椭圆于A、B两点,△ABF是正三角形.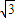 ,0)作直线l与椭圆C交于不同的两点P、Q,且满足
,0)作直线l与椭圆C交于不同的两点P、Q,且满足 ,O是坐标原点.当△OPQ的面积最大时,求椭圆的方程.
,O是坐标原点.当△OPQ的面积最大时,求椭圆的方程.