Question

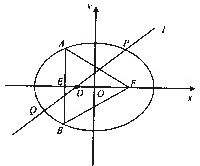（2012•九江一模）设点E、F分别是椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）的左、右焦点，过点E垂直于椭圆长轴的直线交椭圆于A、B两点，△ABF是正三角形．
（1）求椭圆的离心率；
（2）过定点D（-

3

，0）作直线l与椭圆C交于不同的两点P、Q，且满足

DP

=2

QD

，O是坐标原点．当△OPQ的面积最大时，求椭圆的方程．

Answer 1

分析：（1）设椭圆的半焦距为c，则 直线AB的方程为x=-c，将x=-c代入椭圆方程，求得|AB|=

2b2

a

，|EF|=2c，根据△ABF是正三角形，可得

3

2

|AB|=|EF|，从而可求椭圆的离心率；
（2）由（1）知可得椭圆的方程为2x²+3y²=6c²，设直线l的方程为y=k（x+

3

），代入椭圆方程，利用韦达定理及

DP

=2

QD

确定P，Q坐标之间的关系，表示出面积，利用基本不等式求出S_△OPQ的最大值，即可得到椭圆的方程．

解答：解：（1）设椭圆的半焦距为c，则 直线AB的方程为x=-c，将x=-c代入椭圆方程

x2

a2

+

y2

b2

=1，注意到c²=a²-b²，解得y=±

b2

a

，所以|AB|=

2b2

a

，|EF|=2c
∵△ABF是正三角形，∴

3

2

|AB|=|EF|
∴

3

2

×

2b2

a

=2c
∵e=

c

a

，b²=a²-c²，
∴

3

e²+2e-

3

=0
∴e=

3

3

或e=-

3

（舍去）
故所求椭圆的离心率为e=

3

3

（2）由（1）知，a²=3c²，b²=2c²，∴椭圆的方程为2x²+3y²=6c²，①
显然，直线l的斜率不为0
若直线l与x轴垂直，此时P，Q关于x轴对称，

DP

=

QD

，不合题意；
因此，可设直线l的方程为y=k（x+

3

）②，
将②代入①中整理得（3k²+2）x²+6

3

k²x+9k²-6c²=0
因为直线l与椭圆交于P，Q两点，所以△=24（3k²c²-3k²+2c²）＞0
设P（x₁，y₁），Q（x₂，y₂），则x₁+x₂=-

6 3 k2

3k2+2

④，x₁x₂=

9k2-6c2

3k2+2

⑤
由

DP

=2

QD

得（x₁+

3

，y₁）=2（-

3

-x₂，-y₂），∴

x1+ 3 =-2(x2+ 3 ) y1=-2y2

⑥
由④⑥得x1=

-3 3 k2+6 3

3k2+2

，x2=

-3 3 k2-6 3

3k2+2

⑦
∴S_△OPQ=

3

2

|y₁-y₂|=

3

2

|x₁-x₂|=18×

|k|

3k2+2

=18×

1

3|k|+ 2 |k|

≤

3 6

2

当且仅当3|k|=

2

|k|

，即k²=

2

3

时，等号成立
∴k²=

2

3

时，S_△OPQ取得最大值
由⑦求得x₁=

3

，x₂=-2

3

，代入⑤，求得c²=5，满足③
故所求椭圆的方程为2x²+3y²=30，即

x2

15

+

y2

10

=1

点评：本题考查椭圆的几何性质，考查椭圆的标准方程，解题的关键是确定几何量之间的关系，利用直线与椭圆联立，结合韦达定理求解．