题目内容
①点P在△ABC所在的平面内,且 ;②点P为△ABC内的一点,且使得
;②点P为△ABC内的一点,且使得 取得最小值;③点P是△ABC所在平面内一点,且
取得最小值;③点P是△ABC所在平面内一点,且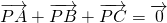 ,上述三个点P中,是△ABC的重心的有
,上述三个点P中,是△ABC的重心的有
- A.0个
- B.1个
- C.2个
- D.3个
D
分析:本题考查的知识点是重心的性质,及向量加减法运算的几何意义,我们可以逐一的对四个结论进行判断,再结合三角形重心的定义,易得答案.
解答:①中,点P在△ABC所在的平面内,
且 ;
;
表示P点既在BC边的中线上,也在AC边的中线上,
根据重心的定义,故①正确;
②中,点P为△ABC内的一点,且使得 取得最小值,
取得最小值,
根据重心的性质,可得②也正确;
③中P是△ABC所在平面内一点,且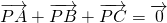 ,
,
这是重心最重要的性质,故③也正确
故三个结论都可以得到P为三角形的重心
故选D
点评:判断P点是否是三角形的重心有如下几种办法:①定义:三条中线的交点.②性质: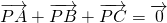 或
或 取得最小值③坐标法:P点坐标是三个顶点坐标的平均数.
取得最小值③坐标法:P点坐标是三个顶点坐标的平均数.
分析:本题考查的知识点是重心的性质,及向量加减法运算的几何意义,我们可以逐一的对四个结论进行判断,再结合三角形重心的定义,易得答案.
解答:①中,点P在△ABC所在的平面内,
且
 ;
;表示P点既在BC边的中线上,也在AC边的中线上,
根据重心的定义,故①正确;
②中,点P为△ABC内的一点,且使得
 取得最小值,
取得最小值,根据重心的性质,可得②也正确;
③中P是△ABC所在平面内一点,且
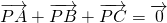 ,
,这是重心最重要的性质,故③也正确
故三个结论都可以得到P为三角形的重心
故选D
点评:判断P点是否是三角形的重心有如下几种办法:①定义:三条中线的交点.②性质:
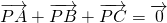 或
或 取得最小值③坐标法:P点坐标是三个顶点坐标的平均数.
取得最小值③坐标法:P点坐标是三个顶点坐标的平均数. 
练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目