题目内容
7.已知函数f(x)=(1+$\sqrt{3}$tan2x)cos2x.(1)求函数f(x)的定义域;
(2)求函数f(x)在区间[-$\frac{π}{6}$,$\frac{π}{6}$]上的最大值和最小值;
(3)求函数f(x)的单调递增区间.
分析 (1)由条件利用正切函数的定义域求得f(x)的定义域.
(2)利用三角恒等变换化简函数的解析式,再利用正弦函数的定义域和值域求得f(x)的最值.
(3)根据正弦函数的增区间,求得f(x)的增区间.
解答 解:(1)对于函数f(x)=(1+$\sqrt{3}$tan2x)cos2x,由2x≠kπ+$\frac{π}{2}$,k∈Z,
求得 x≠$\frac{kπ}{2}$+$\frac{π}{4}$,可得函数的定义域为{x|x≠$\frac{kπ}{2}$+$\frac{π}{4}$,k∈Z}.
(2)∵(x)=(1+$\sqrt{3}$tan2x)cos2x=cos2x+$\sqrt{3}$sin2x=2sin(2x+$\frac{π}{6}$),
又∵x∈[-$\frac{π}{6}$,$\frac{π}{6}$],∴2x+$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{π}{2}$],
故当2x+$\frac{π}{6}$=-$\frac{π}{6}$时,函数f(x)取得最小值为-1,当2x+$\frac{π}{6}$=$\frac{π}{2}$时,函数f(x)取得最大值为2.
(3)令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,求得kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,
可得函数的增区间为[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z.
点评 本题主要考查正切函数的定义域,三角恒等变换,正弦函数的定义域和值域、单调区间,属于中档题.

练习册系列答案
相关题目
18.已知等比数列{an}中,若a4=10,a8=$\frac{5}{2}$,那么a6=( )
| A. | -5 | B. | 5 | C. | ±5 | D. | 25 |
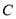
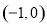 ,以
,以 为圆心的圆与直线
为圆心的圆与直线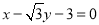 相切.
相切.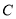 的方程;
的方程;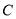 上存在两点关于直线
上存在两点关于直线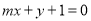 对称,求
对称,求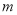 的值.
的值.