题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,已知角A,B,C成等差数列.
(1)若b=
,求a+c的取值范围;
(2)若
,
,
也成等差数列,求证:a=c.
(1)若b=
| ||
| 2 |
(2)若
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
考点:等差数列的性质,正弦定理
专题:综合题,等差数列与等比数列,解三角形
分析:(1)由已知得B=60°,由正弦定理得a+c=sinA+sinC=sinA+sin(1200-A)=
cos(600-A),利用A的范围,即可求a+c的取值范围;
(2)若
,
,
成等差数列,
=
+
,得b=
,结合b2=a2+c2-2accos60°=a2+c2-ac,化简可得a=c.
| 3 |
(2)若
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 2 |
| b |
| 1 |
| a |
| 1 |
| c |
| 2ac |
| a+c |
解答:
(1)解:由已知得B=60°.
由正弦定理
=
=
=
=1,得a+c=sinA+sinC=sinA+sin(1200-A)=
cos(600-A),
∵A∈(0°,120°),∴60°-A∈(-60°,60°),则cos(600-A)∈(
,1],
因此a+c∈(
,
].
(2)证明:由已知
=
+
,得b=
.
又b2=a2+c2-2accos60°=a2+c2-ac,
将b=
代入此式得(
)2=a2+c2-ac,
化简此式得(a2+c2)2+ac(a2+c2)-6a2c2=0,
即(a2+c2+3ac)(a2+c2-2ac)=0.
∵a2+c2+3ac>0,∴a2+c2-2ac=0,得a=c.
由正弦定理
| a |
| sinA |
| c |
| sinC |
| b |
| sinB |
| ||||
| sin600 |
| 3 |
∵A∈(0°,120°),∴60°-A∈(-60°,60°),则cos(600-A)∈(
| 1 |
| 2 |
因此a+c∈(
| ||
| 2 |
| 3 |
(2)证明:由已知
| 2 |
| b |
| 1 |
| a |
| 1 |
| c |
| 2ac |
| a+c |
又b2=a2+c2-2accos60°=a2+c2-ac,
将b=
| 2ac |
| a+c |
| 2ac |
| a+c |
化简此式得(a2+c2)2+ac(a2+c2)-6a2c2=0,
即(a2+c2+3ac)(a2+c2-2ac)=0.
∵a2+c2+3ac>0,∴a2+c2-2ac=0,得a=c.
点评:本题考查正弦定理、余弦定理,考查等差数列的性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
x2=49的充分必要条件是( )
| A、x=7 |
| B、x=-7 |
| C、x=7或x=-7 |
| D、x=7且x=-7 |
在3与27之间插入7个数,使它们成为等差数列,则插入的7个数的第四个数是( )
| A、18 | B、9 | C、12 | D、15 |
在下列函数中,最小值为2的是( )
A、y=
| ||||||
B、y=lgx+
| ||||||
C、y=x+
| ||||||
| D、y=x2-2x+4 |
 如图,平面直角坐标系中,动点P(x,y),PM⊥y轴,垂足为M,点N与点P关于x轴对称,且
如图,平面直角坐标系中,动点P(x,y),PM⊥y轴,垂足为M,点N与点P关于x轴对称,且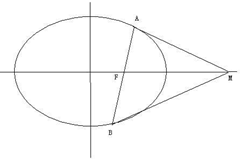 如图,椭圆
如图,椭圆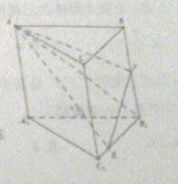 如图,已知三棱柱ABC-A1B1C1中BB1⊥平面ABC,且AC⊥BC1,AA1=3,AC=CB=2.E,F分别为线段B1C1,BB1上的动点.
如图,已知三棱柱ABC-A1B1C1中BB1⊥平面ABC,且AC⊥BC1,AA1=3,AC=CB=2.E,F分别为线段B1C1,BB1上的动点.