题目内容
直线l过点M(1,1),与椭圆| x2 |
| 4 |
| y2 |
| 3 |
分析:由于A,B两点是直线与椭圆的交点,故他们应满足椭圆方程,设出它们的坐标,然后根据它们的中点为M,可将坐标间的关系转化为求直线l的斜率,然后再由点斜式求出直线方程.
解答:解:设A(x1,y1)、B(x2,y2),
则
+
=1,①
+
=1.②
①-②,得
+
=0.
∴
=-
•
.
又∵M为AB中点,
∴x1+x2=2,y1+y2=2.
∴直线l的斜率为-
.
∴直线l的方程为y-1=-
(x-1),
即3x+4y-7=0.
则
| ||
| 4 |
| ||
| 3 |
| ||
| 4 |
| ||
| 3 |
①-②,得
| (x1-x2)(x1+x2) |
| 4 |
| (y1-y2)(y1+y2) |
| 3 |
∴
| y1-y2 |
| x1-x2 |
| 3 |
| 4 |
| x1+x2 |
| y1+y2 |
又∵M为AB中点,
∴x1+x2=2,y1+y2=2.
∴直线l的斜率为-
| 3 |
| 4 |
∴直线l的方程为y-1=-
| 3 |
| 4 |
即3x+4y-7=0.
点评:在求直线方程时,应先选择适当的直线方程的形式,并注意各种形式的适用条件,用斜截式及点斜式时,直线的斜率必须存在,而两点式不能表示与坐标轴垂直的直线,截距式不能表示与坐标轴垂直或经过原点的直线,故在解题时,若采用截距式,应注意分类讨论,判断截距是否为零;若采用点斜式,应先考虑斜率不存在的情况.

练习册系列答案
相关题目
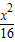 +
+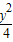 =1交于P,Q两点,已知线段PQ的中点横坐标为
=1交于P,Q两点,已知线段PQ的中点横坐标为 ,求直线l的方程.
,求直线l的方程.