题目内容
直线l过点M(1,1),与椭圆
+
=1交于P,Q两点,已知线段PQ的中点横坐标为
,求直线l的方程.
| x2 |
| 16 |
| y2 |
| 4 |
| 1 |
| 2 |
分析:平方差法:易判断直线存在斜率,设P(x1,y1),Q(x2,y2),PQ的中点为(
,y0),把P、Q坐标代入椭圆方程两式相减,利用斜率公式及中点坐标公式可用y0表示出直线斜率,再用M点坐标及中点的坐标可表示出斜率,从而得到关于y0的方程,解出y0后即可求得斜率,用点斜式即可求得直线方程.
| 1 |
| 2 |
解答:解:易知直线l存在斜率,
设P(x1,y1),Q(x2,y2),PQ的中点为(
,y0),则x1+x2=1,y1+y2=2y0,
把P、Q坐标代入椭圆方程,得
+
=1①,
+
=1②,
①-②得,
+
=0,即
=-
=-
,
又
=
,
所以
=-
,解得y0=
+
,y0=
-
,
则直线斜率k=-
=1±
,
所以直线l方程为:y-1=(1+
)(x-1)或y-1=(1-
)(x-1),即y=(1+
)(x-1)+1或y=(1-
)(x-1)+1.
设P(x1,y1),Q(x2,y2),PQ的中点为(
| 1 |
| 2 |
把P、Q坐标代入椭圆方程,得
| x12 |
| 16 |
| y12 |
| 4 |
| x22 |
| 16 |
| y22 |
| 4 |
①-②得,
| x12-x22 |
| 16 |
| y12-y22 |
| 4 |
| y1-y2 |
| x1-x2 |
| x1+x2 |
| 4(y1+y2) |
| 1 |
| 8y0 |
又
| y1-y2 |
| x1-x2 |
| y0-1 | ||
|
所以
| y0-1 | ||
|
| 1 |
| 8y0 |
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
| ||
| 4 |
则直线斜率k=-
| 1 |
| 8y0 |
| ||
| 2 |
所以直线l方程为:y-1=(1+
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
点评:本题考查直线与圆锥曲线的位置关系,属中档题,凡涉及弦中点问题可用平方差法解决.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
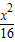 +
+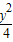 =1交于P,Q两点,已知线段PQ的中点横坐标为
=1交于P,Q两点,已知线段PQ的中点横坐标为 ,求直线l的方程.
,求直线l的方程.