题目内容
直线l过点M(1,1),与椭圆
+
=1相交于A、B两点,若AB的中点为M,试求直线l的方程.
| x2 |
| 4 |
| y2 |
| 3 |
设A(x1,y1)、B(x2,y2),
则
+
=1,①
+
=1.②
①-②,得
+
=0.
∴
=-
•
.
又∵M为AB中点,
∴x1+x2=2,y1+y2=2.
∴直线l的斜率为-
.
∴直线l的方程为y-1=-
(x-1),
即3x+4y-7=0.
则
| ||
| 4 |
| ||
| 3 |
| ||
| 4 |
| ||
| 3 |
①-②,得
| (x1-x2)(x1+x2) |
| 4 |
| (y1-y2)(y1+y2) |
| 3 |
∴
| y1-y2 |
| x1-x2 |
| 3 |
| 4 |
| x1+x2 |
| y1+y2 |
又∵M为AB中点,
∴x1+x2=2,y1+y2=2.
∴直线l的斜率为-
| 3 |
| 4 |
∴直线l的方程为y-1=-
| 3 |
| 4 |
即3x+4y-7=0.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
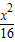 +
+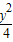 =1交于P,Q两点,已知线段PQ的中点横坐标为
=1交于P,Q两点,已知线段PQ的中点横坐标为 ,求直线l的方程.
,求直线l的方程.