题目内容
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
设二次函数![]() ,对任意实数
,对任意实数![]() ,
,![]() 恒成立;数列
恒成立;数列![]() 满足
满足![]() .
.
(1)求函数![]() 的解析式和值域;
的解析式和值域;
(2)试写出一个区间![]() ,使得当
,使得当![]() 时,数列
时,数列![]() 在这个区间上是递增数列,
在这个区间上是递增数列,
并说明理由;
(3)已知![]() ,求:
,求: .
.
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
解:(1)由![]() 恒成立等价于
恒成立等价于![]() 恒成立,…………………………1分
恒成立,…………………………1分
从而得: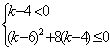 ,化简得
,化简得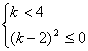 ,从而得
,从而得![]() ,所以
,所以![]() ,………3分
,………3分
其值域为![]() .………………………………………………………………………………………………4分
.………………………………………………………………………………………………4分
(2)解:当![]() 时,数列
时,数列![]() 在这个区间上是递增数列,证明如下:
在这个区间上是递增数列,证明如下:
设![]() ,则
,则![]() ,所以对一切
,所以对一切![]() ,均有
,均有![]() ;………………………………………………………………………………………………7分
;………………………………………………………………………………………………7分
![]()
![]() ,
,
从而得![]() ,即
,即![]() ,所以数列
,所以数列![]() 在区间
在区间![]() 上是递增数列.………………………10分
上是递增数列.………………………10分
注:本题的区间也可以是![]() 、
、![]() 、
、![]() 等无穷多个.
等无穷多个.
另解:若数列![]() 在某个区间上是递增数列,则
在某个区间上是递增数列,则![]()
即![]()
![]() …………………………7分
…………………………7分
又当![]() 时,
时,![]() ,所以对一切
,所以对一切![]() ,均有
,均有![]() 且
且![]() ,所以数列
,所以数列![]() 在区间
在区间![]() 上是递增数列.…………………………10分
上是递增数列.…………………………10分
(3)(文科)由(2)知![]() ,从而
,从而![]() ;
;
![]() ,即
,即![]() ; ………12分
; ………12分
令![]() ,则有
,则有![]() 且
且![]() ;
;
从而有![]() ,可得
,可得![]() ,所以数列
,所以数列![]() 是以
是以![]() 为首项,公比为
为首项,公比为![]() 的等比数列,……………………………………14分
的等比数列,……………………………………14分
从而得 ,即
,即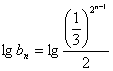 ,所以
,所以 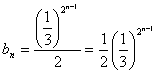 ,
,
所以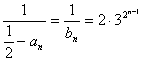 ,所以
,所以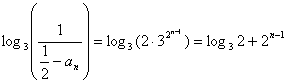 , ………………16分
, ………………16分
所以,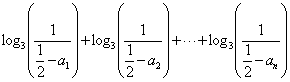
![]() . ……………………………………………………18分
. ……………………………………………………18分
(3)(理科)由(2)知![]() ,从而
,从而![]() ;
;
![]() ,即
,即![]() ;………12分
;………12分
令![]() ,则有
,则有![]() 且
且![]() ;
;
从而有![]() ,可得
,可得![]() ,所以数列
,所以数列![]() 是
是![]() 为首项,公比为
为首项,公比为![]() 的等比数列,………………………………………………………14分
的等比数列,………………………………………………………14分
从而得 ,即
,即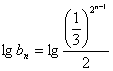 ,所以
,所以 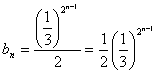 ,
,
所以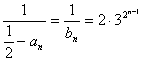 ,所以
,所以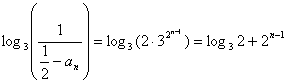 ,
,
所以,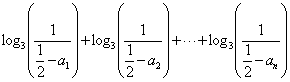
![]() .………………………………………………………16分
.………………………………………………………16分
即![]()
![]()
![]() ,所以,
,所以,![]() 恒成立
恒成立
当![]() 为奇数时,即
为奇数时,即![]() 恒成立,当且仅当
恒成立,当且仅当![]() 时,
时,![]() 有最小值
有最小值![]() 为。
为。![]()
当![]() 为偶数时,即
为偶数时,即![]() 恒成立,当且仅当
恒成立,当且仅当![]() 时,有最大值
时,有最大值![]() 为。
为。![]()
所以,对任意![]() ,有
,有![]() 。又
。又![]() 非零整数,
非零整数,![]() …………………………………18分
…………………………………18分

 和正数
和正数 ,且对任意的正整数n,当
,且对任意的正整数n,当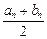 ≥0时, 有[
≥0时, 有[ ,
,  ]=
]= ,
, 
 ].
]. }是等比数列;
}是等比数列; ,求证
,求证
 ;
; ,使得数列
,使得数列 为常数数列?请说明理由
为常数数列?请说明理由 到其准线的距离等于5.
到其准线的距离等于5. 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值; 且
且 与
与 面积之和的最小值.
面积之和的最小值.
 ,对于项数为
,对于项数为 的有穷数列
的有穷数列 ,令
,令 为
为 中最大值,称数列
中最大值,称数列 为
为 3,5,4,7的创新数列为3,5,5,7.
3,5,4,7的创新数列为3,5,5,7. 的所有排列,将每种排列都视为一个有穷数列
的所有排列,将每种排列都视为一个有穷数列 .
. ,写出创新数列为3,4,4,4的所有数列
,写出创新数列为3,4,4,4的所有数列 的首项为1,前
的首项为1,前 项和为
项和为 ,且满足
,且满足 ,
, .数列
.数列 满足
满足 .
.  时,试比较
时,试比较 与
与 的大小,并说明理由;
的大小,并说明理由;
 是否可能恰为直线
是否可能恰为直线
 的方向向量?请说明你的理由.
的方向向量?请说明你的理由.