题目内容
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为 ![]() . (Ⅰ)求椭圆C的方程;
. (Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为 ![]() ,求△AOB面积的最大值.
,求△AOB面积的最大值.
【答案】解:(Ⅰ)设椭圆的半焦距为c,依题意 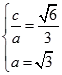 ∴b=1,∴所求椭圆方程为
∴b=1,∴所求椭圆方程为 ![]() . (Ⅱ)设A(x1 , y1),B(x2 , y2).
. (Ⅱ)设A(x1 , y1),B(x2 , y2).
①当AB⊥x轴时, ![]() .
.
②当AB与x轴不垂直时,设直线AB的方程为y=kx+m.
由已知 ![]() ,得
,得 ![]() .
.
把y=kx+m代入椭圆方程,整理得(3k2+1)x2+6kmx+3m2﹣3=0,
∴ ![]() ,
, ![]() .
.
∴|AB|2=(1+k2)(x2﹣x1)2
= 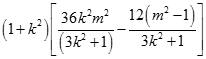
= 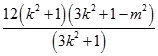
= 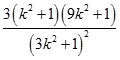
= ![]()
= 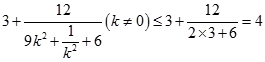 .
.
当且仅当 ![]() ,即
,即 ![]() 时等号成立.当k=0时,
时等号成立.当k=0时, ![]() ,
,
综上所述|AB|max=2.∴当|AB|最大时,△AOB面积取最大值 ![]()
【解析】(Ⅰ)设椭圆的半焦距为c,依题意求出a,b的值,从而得到所求椭圆的方程.(Ⅱ)设A(x1 , y1),B(x2 , y2).(1)当AB⊥x轴时, ![]() .(2)当AB与x轴不垂直时,设直线AB的方程为y=kx+m.由已知
.(2)当AB与x轴不垂直时,设直线AB的方程为y=kx+m.由已知 ![]() ,得
,得 ![]() .把y=kx+m代入椭圆方程,整理得(3k2+1)x2+6kmx+3m2﹣3=0,然后由根与系数的关系进行求解.
.把y=kx+m代入椭圆方程,整理得(3k2+1)x2+6kmx+3m2﹣3=0,然后由根与系数的关系进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目