题目内容
【题目】设函数f（x）=4sinx（cosx﹣sinx）+3 （Ⅰ）当x∈（0，π）时，求f（x）的单调递减区间；
（Ⅱ）若f（x）在[0，θ]上的值域为[0，2 
+1]，求cos2θ的值．
【答案】解：（Ⅰ）函数f（x）=4sinx（cosx﹣sinx）+3
=4sinxcosx﹣4sin2x+3
=2sin2x﹣4× 
+3
=2sin2x+2cos2x+1
=2 
sin（2x+ 
）+1，
令2kπ+ 
≤2x+ ≤2kπ+ 
，k∈Z，
解得kπ+ 
≤x≤kπ+ 
，k∈Z，
又x∈（0，π），
所以f（x）的单调递减区间是[ ， ]；
（Ⅱ）由f（x）=2 sin（2x+ ）+1在[0，θ]上的值域为[0，2 +1]，
令x=0，得f（0）=2 sin +1=3；
令f（x）=2 +1，得sin（2x+ ）=1，
解得x= ，∴θ＞ ；
令f（x）=0，得sin（2x+ ）=﹣ 
，
∴2x+ ＜ ，
解得x＜ ，即θ＜ ；
∴θ∈（ ， 
），
∴2θ+ ∈（ ， 
）；
由2 
sin（2θ+ ）+1=0，
得sin（2θ+ ）=﹣ 
，
所以cos（2θ+ ）=﹣ 
=﹣ 
，
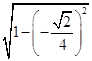所以cos2θ=cos[（2θ+ ）﹣ ]
=cos（2θ+ ）cos +sin（2θ+ ）sin
=﹣ × 
+（﹣ ）×
=﹣ 
．
【解析】（Ⅰ）化简函数f（x）为正弦型函数，根据正弦函数的图象与性质即可求出f（x）的单调减区间；（Ⅱ）根据题意，求出sin（2θ+ 
）的值，再根据同角的三角函数关系和三角恒等变换求出cos2θ的值．
【考点精析】根据题目的已知条件，利用正弦函数的单调性的相关知识可以得到问题的答案，需要掌握正弦函数的单调性：在
上是增函数；在
上是减函数．
