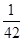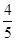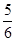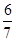题目内容
已知数列{an}的前n项和为Sn,对任意的n∈N*有Sn= an-
an- ,且1<Sk<12,则k的值为( )
,且1<Sk<12,则k的值为( )
 an-
an- ,且1<Sk<12,则k的值为( )
,且1<Sk<12,则k的值为( )| A.2 | B.2或4 | C.3或4 | D.6 |
B
本题考查等比数列的前n项和,考查考生对数列知识的综合运用能力,属于中档题.首先要根据Sn= an-
an- ,推出数列{an}是等比数列并求出其通项公式,然后用前n项和公式表达出Sn,再对选项中k的值逐一进行验证.
,推出数列{an}是等比数列并求出其通项公式,然后用前n项和公式表达出Sn,再对选项中k的值逐一进行验证.
∵a1= a1-
a1- ,∴a1=-2.∵an+1=Sn+1-Sn=
,∴a1=-2.∵an+1=Sn+1-Sn= (an+1-an),∴an+1=-2an,数列{an}是以-2为首项,-2为公比的等比数列,∴an=(-2)n,Sn=
(an+1-an),∴an+1=-2an,数列{an}是以-2为首项,-2为公比的等比数列,∴an=(-2)n,Sn= (-2)n-
(-2)n- .逐一检验即可知k=4或2.
.逐一检验即可知k=4或2.
 an-
an- ,推出数列{an}是等比数列并求出其通项公式,然后用前n项和公式表达出Sn,再对选项中k的值逐一进行验证.
,推出数列{an}是等比数列并求出其通项公式,然后用前n项和公式表达出Sn,再对选项中k的值逐一进行验证.∵a1=
 a1-
a1- ,∴a1=-2.∵an+1=Sn+1-Sn=
,∴a1=-2.∵an+1=Sn+1-Sn= (an+1-an),∴an+1=-2an,数列{an}是以-2为首项,-2为公比的等比数列,∴an=(-2)n,Sn=
(an+1-an),∴an+1=-2an,数列{an}是以-2为首项,-2为公比的等比数列,∴an=(-2)n,Sn= (-2)n-
(-2)n- .逐一检验即可知k=4或2.
.逐一检验即可知k=4或2.
练习册系列答案
相关题目
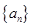 的前
的前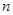 项和为
项和为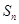 ,且
,且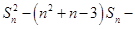
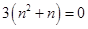 ,
,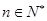 .
.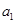 的值;
的值;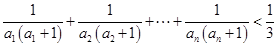 .
.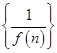 (n∈N*)的前n项和是( )
(n∈N*)的前n项和是( )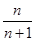
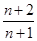
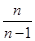
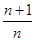
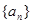 中,
中,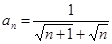 (其中
(其中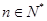 ),若其前n项和
),若其前n项和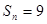 ,则
,则 .
. 的前
的前 项和为
项和为 ,若
,若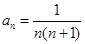 ,则
,则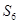 等于( )
等于( )