题目内容
在直角坐标系xOy中,曲线C1的参数方程为:
(θ为参数),以直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:ρ(2cosθ-sinθ)=6.
(Ⅰ)试写出直线l的直角坐标方程和曲线C1的普通方程;
(Ⅱ)在曲线C1上求一点P,使点P到直线l的距离最大,并求出此最大值.
|
(Ⅰ)试写出直线l的直角坐标方程和曲线C1的普通方程;
(Ⅱ)在曲线C1上求一点P,使点P到直线l的距离最大,并求出此最大值.
考点:参数方程化成普通方程
专题:选作题,坐标系和参数方程
分析:(Ⅰ)根据x=ρcosθ,y=ρsinθ把直线l的极坐标方程化为直角坐标方程,利用同角三角函数的基本关系把曲线C1的参数方程化为直角坐标方程.
(Ⅱ)设点P(
cosθ,2sinθ),求得点P到直线l的距离为d=
,利用正弦函数的值域求得d的最大值.
(Ⅱ)设点P(
| 3 |
|4sin(
| ||
|
解答:
解:(Ⅰ)直线l的方程为:ρ(2cosθ-sinθ)=6,即 2x-y-6=0.
曲线C1的参数方程为:
(θ为参数),普通方程为
+
=1;
(Ⅱ)设点P(
cosθ,2sinθ),
则点P到直线l的距离为d=
=
,
故当sin(
-θ)=-1时,d取得最大值为2
.
曲线C1的参数方程为:
|
| x2 |
| 3 |
| y2 |
| 4 |
(Ⅱ)设点P(
| 3 |
则点P到直线l的距离为d=
|4sin(
| ||
|
|4sin(
| ||
|
故当sin(
| π |
| 3 |
| 5 |
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,两角和的正弦公式、正弦函数的值域,属于基础题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 已知四边形ABCD是菱形,DA=DB=2,DD1⊥面ABCD,点P为线段OD1上的任一点.
已知四边形ABCD是菱形,DA=DB=2,DD1⊥面ABCD,点P为线段OD1上的任一点.
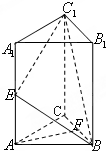 如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=4,E、F分别为AA1、BC的中点.
如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=4,E、F分别为AA1、BC的中点.